4.1. САУ положением инвертированного маятника

Объект управления представляет собой груз массой $m$ на стержне длиной $L$ , нижний конец которого шарнирно закреплен на ленте транспортера. Массой стержня, по сравнению с массой маятника $m$ , можно пренебречь. Лента приводится в движение двигателем постоянного тока (ДПТ) и может перемещаться вдоль плоскости вращения стержня. Задача состоит в выборе такого управления электродвигателем, которое обеспечивает удержание маятника в вертикальном положении. Модель системы управления положением перевернутого маятника представлена на рис.4.1. Требуется с помощью управления ДПТ, перемещающей ленту с шарнирно закрепленным стержнем в горизонтальной плоскости, удержать неустойчивый маятник в вертикальном положении.

Рис.4.1. Схема инвертированного маятника.

Положение инвертированного маятника относительно вертикальной оси $θ$ измеряется при помощи датчика угла поворота, встроенного в опору стержня. Управление осуществляется при помощи нечеткого контроллера, который углу поворота $θ$ и производной угла поворота $\dot{θ}$ стержня маятника относительно вертикальной оси осуществляет нечеткий вывод и синтезирует управление $u$ . Тиристорный усилитель преобразует управление $u$ в напряжение питания $u_{дв}$ ДПТ.

Известная система уравнений, описывающих движение маятника, состоящая из уравнений динамики вращательного движения груза m относительно шарнирной опоры маятника и динамики поступательного движения груза m относительно горизонтальной оси выглядит следующим образом [40]:

\{\begin{matrix} mL^{2}\overset{..}{θ} = mLgsinθ - mL\dot{x}cosθ - ξ\dot{θ}, \\ m\overset{..}{x} = mLθ^{2}sinθ - mL\dot{θ}cosθ - μ\dot{x} - F, \end{matrix}

где

ξ -

коэффициент трения в опоре маятника,

μ -

коэффициент сопротивления среды

F -

сила, прилагаема к опоре маятника под действием электропривода. Поскольку сила, прилагаемая электроприводом к опоре маятника пропорциональна напряжению питания электродвигателя, а динамика переходного процесса по каналу

\frac{F}{u_{дв}}

определяется параметрами только электромагнитной цепи двигателя и не зависит от электромеханической составляющей, то длительностью переходного процесса в двигателе по каналу

\frac{F}{u_{дв}}

можно пренебречь. Также можно пренебречь длительностью переходных процессов в тиристорном усилителе. Таким образом сила, развиваемая электроприводом и прилагаемая к опоре маятника

F = ku

, где k – коэффициент усиления электропривода. Структурная схема нечеткой САУ положением инвертированного маятника выглядит следующим образом (рис.4.2).

Рис.4.2.Структурная схема нечеткой САУ положением инвертированного маятника

Лингвистические переменные «угол отклонения» и «угловая скорость отклонения», соответствующие входам нечеткого контроллера θ и $\dot{θ}$ , по модулю ограничиваются нелинейными элементами с насыщением $∣ θ ∣ \leq 0,7 рад$ , $∣ \dot{θ} ∣ \leq 2 рад$ и задаются термами NB-«отрицательная большая», N-«отрицательная», Z-«нулевая», P-«положительная», PB-«положительная большая» (рис.4.3).

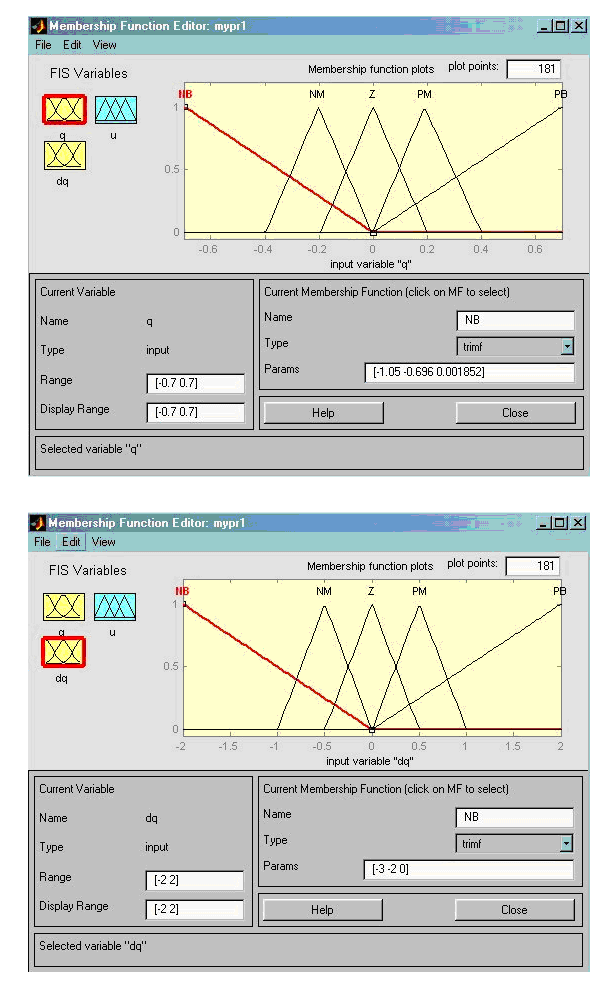
Рис.4.3. Функции принадлежностей лингвистических переменных, определяющих нечеткое представление входных сигналов нечеткого контроллера

Лингвистическая переменная «управление», соответствующая выходу нечеткого контроллера , задается термами NB-«отрицательная большая», N-«отрицательная», Z-«нулевая», P-«положительная», PB-«положительная большая» на конечном интервале, соответствующем физическим ограничениям тиристорного усилителя (рис.4.4).

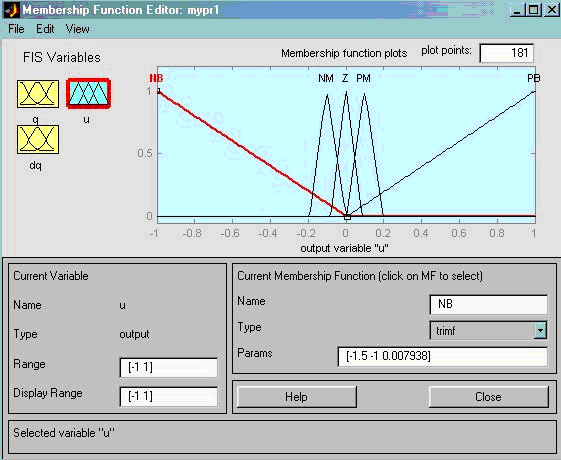
Рис.4.4. Функции принадлежностей лингвистических переменных, определяющих нечеткое представление выходного сигнала нечеткого контроллера

Лингвистические правила, которыми следует руководствоваться при выборе нечеткого значения управления u сведены в таблицу 3.4.

Таблица 3.4

Из таблицы видно, что база нечетких правил определена не полностью на всем пространстве значений нечетких переменных, поэтому при программировании нечеткого контроллера соответствующая часть правил не вводится (рис.4.5).

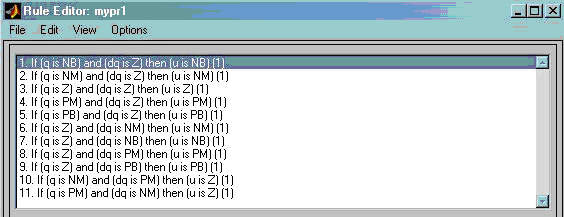
Рис.4.5. База правил нечеткого контроллера

Структура системы управления (рис.4.2) представляет собой САУ с двухвходовым нечетким контроллером с зависимыми входами, что делает возможным при анализе динамики системы представление нечеткого контроллера эквивалентным нелинейным элементом с одним входом и выходом. Сигнал задания требуемого значения выходной величины θ отсутствует, поскольку ее значение задается неявно в виде цели управления (стабилизации положения маятника, т.е. θ=0 ) при формулировке базы продукционных правил системы нечеткого вывода.

Зададимся следующими параметрами модели объекта управления (3.2): $m = 0,074 кг$ , $L = 0,5 м$ , $ξ = 0,002 кг⋅м^{2}/ c$ , $μ = 2 кг / c$ , $k = 5$ ; и проведем имитационное моделирование нечеткой САУ (рис.4.2) с контроллером Мамдани в режиме, соответствующем перемещению на расстояние 1,3 м в строну от исходного положения опоры маятника, с учетом того, что на опору маятника действуют случайные помехи, вызывающие ее отклонения ∆θ , распределенные равномерно в интервале $[-0,01; 0,01]$ .

Результаты моделирования, представленные на рис.4.6 говорят о том, что с задачами перемещения в пространстве и одновременной балансировки перевернутого маятника при наличии случайных помех нечеткая система справляется не менее успешно, чем это сделал бы человек, перемещая на своей раскрытой ладони вертикально стоящий тонкий стержень, к примеру, металлический прут. Таким образом, можно сказать, что рассмотренная нечеткая система управления в ходе своей работы фактически воспроизводит человеческие реакции на отклонение объекта от состояния равновесия, поскольку руководствуется теми же правилами, что и человек, вручную балансирующий инверсный маятник.

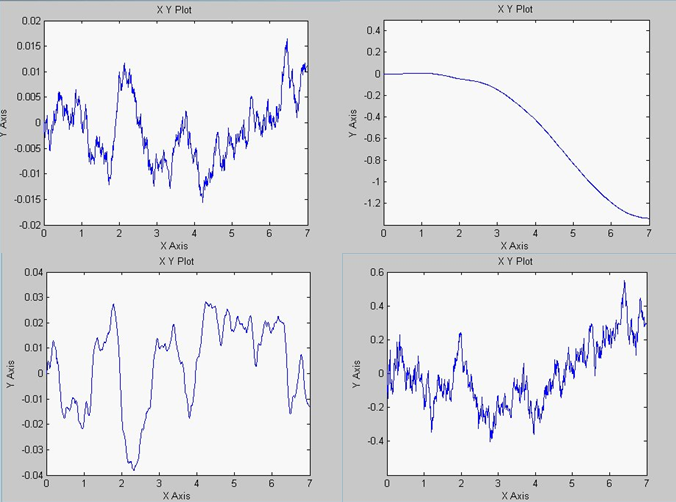
Рис.4.6. Результаты моделирования динамики нечеткой САУ слева: вверху – угловое отклонение θ, внизу – скорость отклонения θ;справа: вверху – линейное перемещение x ; внизу – управление u