2.4. Расстояние между нечеткими множествами и индексы нечеткости

Пусть $A$ , $B$ и $C$ – конечные нечеткие множества, заданные на универсальном множестве $X$ . Введем понятие расстояния $ρ (A, B)$ между нечеткими множествами. При введении расстояния обычно предъявляются следующие требования:

$ρ (A, B) \geq 0$ – неотрицательность;
$ρ (A, B) = ρ (B, A)$ – симметричность;
$ρ (A, B) \leq ρ (A, C) + ρ (B, C)$ – транзитивность;
$ρ (A, A) = 0$ – самоподобие.

Расстояние Хемминга(линейное расстояние) определяется как:

$ρ (A, B) = \sum_{i = 1}^{n} |μ_{A}(x_{i})-μ_{B}(x_{i})|$ , $0 \leq ρ (A, B) \leq n$ .

Относительное расстояние Хемминга определяется как:

$ρ_{rel} (A, B) = \frac{1}{n} \sum_{i = 1}^{n} |μ_{A}(x_{i})-μ_{B}(x_{i})| = \frac{1}{n} ρ (A, B)$ , $0 \leq ρ_{rel} (A, B) \leq 1$ .

Евклидово (квадратичное расстояние) определяется как:

$e (A, B) = \sqrt{\sum_{i = 1}^{n} {(μ_{A} (x_{i}) - μ_{B} (x_{i}))}^{2}}$ , $0 \leq e (A, B) \leq \sqrt{n}$ .

Относительное Евклидово расстояние определяется как:

$e_{rel} (A, B) = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(μ_{A} (x_{i}) - μ_{B} (x_{i}))}^{2} =} \frac{e (A, B)}{\sqrt{n}}$ , $0 \leq e_{rel} (A, B) \leq 1$ .

В случае бесконечных счетных нечетких множеств $A, B$ расстояние Хемминга и квадратичное расстояние определяются аналогично, с учетом сходимости соответствующих сумм:

$ρ (A, B) = lim_{n \to \infty} \sum_{i = 1}^{n} |μ_{A}(x_{i})-μ_{B}(x_{i})|$ , $ρ_{rel} (A, B) = lim_{n \to \infty} \frac{1}{n} \sum_{i = 1}^{n} |μ_{A}(x_{i})-μ_{B}(x_{i})|$ ,

$e (A, B) = lim_{n \to \infty} \sqrt{\sum_{i = 1}^{n} {(μ_{A} (x_{i}) - μ_{B} (x_{i}))}^{2}}$ , $e_{rel} (A, B) = lim_{n \to \infty} \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(μ_{A} (x_{i}) - μ_{B} (x_{i}))}^{2}}$ .

В случае бесконечных несчетных нечетких множеств $A, B$ , с ограниченным носителем $(a; b)$ , расстояние Хемминга и квадратичное расстояние определяются следующим образом:

$ρ (A, B) = \int_{a}^{b} |μ_{A}(x)-μ_{B}(x)| dx$ , $ρ_{rel} (A, B) = \frac{1}{b - a} \int_{a}^{b} |μ_{A}(x)-μ_{B}(x)| dx$ ,

$e (A, B) = \sqrt{\int_{a}^{b} {(μ_{A} (x) - μ_{B} (x))}^{2} dx}$ , $e_{rel} (A, B) = \sqrt{\frac{1}{b - a} \int_{a}^{b} {(μ_{A} (x) - μ_{B} (x))}^{2} dx}$ .

В случае бесконечных несчетных нечетких множеств $A, B$ , носители которых неограниченны (варианты $(- \infty; a)$ , $(a; \infty)$ , $(- \infty; + \infty)$ , расстояние Хемминга и квадратичное расстояние определяются аналогично с условием сходимости соответствующих несобственных интегралов:

$ρ (A, B) = \int_{- \infty}^{a} |μ_{A}(x)-μ_{B}(x)| dx$ , $ρ (A, B) = \int_{a}^{\infty} |μ_{A}(x)-μ_{B}(x)| dx$ , $ρ (A, B) = \int_{- \infty}^{\infty} |μ_{A}(x)-μ_{B}(x)| dx$ , $e (A, B) = \sqrt{\int_{- \infty}^{a} {(μ_{A} (x) - μ_{B} (x))}^{2} dx}$ , $e (A, B) = \sqrt{\int_{a}^{\infty} {(μ_{A} (x) - μ_{B} (x))}^{2} dx}$ , $e (A, B) = \sqrt{\int_{- \infty}^{\infty} {(μ_{A} (x) - μ_{B} (x))}^{2} dx}$ .

При задании несчетных нечетких множеств с неограниченными носителями относительные оценки $ρ_{rel} (A, B)$ и $e_{rel} (A, B)$ в качестве меры расстояний между нечеткими множествами не используются. Однако, если это необходимо, то относительную меру расстояния можно ввести, используя другое определение или другое понятие сходимости [26].

Выбор того или иного расстояния – абсолютного или относительного, Хемминга или Евклидова зависит от природы рассматриваемой проблемы. Каждое из этих расстояний обладает определенными преимуществами и недостатками, которые становятся очевидными при практическом решении той или иной технической задачи. В зависимости от специфики решаемой проблемы для нечетких множеств можно ввести и другие понятия меры расстояния [17], [26].

Пример. $A = 0,1 / 1 + 0,5 / 2 + 1 / 3$ , $B = 0,2 / 2 + 1 / 3 + 0,7 / 4$ .

$ρ (A, B) = |0,1-0| + |0,5-0,2| + |1-1| + |0-0,7| = 0,1 + 0,3 + 0 + 0,7 = 1,1$ .

$ρ_{rel} (A, B) = \frac{1}{4} (|0,1-0| + |0,5-0,2| + |1-1| + |0-0,7|) = \frac{1}{4} (0,1 + 0,3 + 0 + 0,7) = 0, 275$ .

$e (A, B) = \sqrt{{(0,1 - 0)}^{2} + {(0,5 - 0,2)}^{2} + {(1 - 1)}^{2} + {(0 - 0,7)}^{2}} = \sqrt{0, 01 + 0, 09 + 0 + 0, 49} = 0, 768$ .

$e_{rel} (A, B) = \sqrt{\frac{{(0,1 - 0)}^{2} + {(0,5 - 0,2)}^{2} + {(1 - 1)}^{2} + {(0 - 0,7)}^{2}}{4}} = \sqrt{\frac{0, 01 + 0, 09 + 0 + 0, 49}{4}} = 0, 384$ .

Введем далее индекс нечеткостиили показатель размытости нечеткого множества. Если объект $x$ обладает свойством $R$ , порождающим нечеткое множество $A$ лишь в частной мере, т.е. $0 \leq μ_{A} (x) \leq 1$ , то внутренняя неопределенность, двусмысленность объекта $x$ в отношении свойства $R$ проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов $A$ , обладающих свойством $R$ , и классу объектов $\overset{ˉ}{A}$ , не обладающих свойством $R$ . Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. $μ_{A} (x) = μ_{\overset{ˉ}{A}} (x) = 0,5$ , и минимальна, когда объект принадлежит только одному классу, т.е. либо $μ_{A} (x) = 1$ и $μ_{\overset{ˉ}{A}} (x) = 0$ , либо $μ_{A} (x) = 0$ и $μ_{\overset{ˉ}{A}} (x) = 1$ . В общем случае показатель размытости нечеткого множества $A$ можно определить в виде функционала $d (A)$ , удовлетворяющего следующим условиям:

$d (A) = 0$ тогда, когда $A$ – обычное множество с $μ_{A} (x) \in \{0; 1\}$ ;
$d (A)$ максимально тогда, когда $μ_{A} (x) = 0,5$ для всех $\forall x \in X$ ;
$d (A) \leq d (B)$ , если $A$ является заострением $B$ , т.е. выполняется

\{\begin{matrix} μ_{A} (x) \leq μ_{B} (x), если μ_{B} (x) < 0,5, \\ μ_{A} (x) \geq μ_{B} (x), если μ_{B} (x) > 0,5, \\ μ_{A} (x) \in [0; 1], если μ_{B} (x) = 0,5; \end{matrix}

$d (A) \leq d (\overset{ˉ}{A})$ – симметричность относительно точек перехода;
$d (A \cup B) + d (A \cap B) = d (A) + d (B)$ .

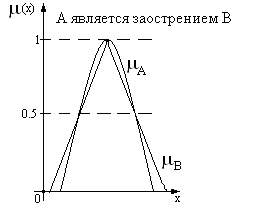
Рис.2.13. Заострение нечеткого множества

Приведенная система аксиом при введении конкретных показателей размытости часто используется частично, т.е., например, ограничиваются только некоторыми условиями, накладывающими ограничения на функционал $d (A)$ , либо некоторые условия усиливаются или ослабляются в зависимости от решаемой задачи. Обычно оперируют индексами нечеткости (показателями размытости), которые можно определить, используя понятие расстояния.

Обычное множество, ближайшее к нечеткому. Пусть $A$ – нечеткое множество, определенное на универсальном множестве $X$ . Какое обычное множество $\underset{ˉ}{A} \subset X$ является ближайшим к $A$ , т.е. находится на наименьшем евклидовом расстоянии от нечеткого множества $A$ ? Такое множество будет обладать следующей характеристической функцией:

μ_{\underline{A}} (x_{i}) = \{\begin{matrix} 0, если μ_{A} (x_{i}) \leq 0,5, \\ 1, если μ_{A} (x_{i}) > 0,5 . \end{matrix}

Обычно принимают $μ_{\underline{A}} (x_{i}) = 0$ если $μ_{A} (x_{i}) = 0,5$ . Используя понятие обычного множества, ближайшего к нечеткому, введем следующие индексы нечеткости нечеткого множества $A$ .

Линейный индекс нечеткости:

$d (A) = \frac{2}{n} ρ (A, \underset{ˉ}{A})$ для конечного нечеткое множества $A$ ;
$d (A) = lim_{n \to \infty} (\frac{2}{n} \sum_{i = 1}^{n} |μ_{A}(x_{i})-μ_{\underline{A}}(x_{i})|)$ для бесконечного счетного нечеткого множества $A$ ;
$d (A) = \frac{2}{b - a} \int_{a}^{b} |μ_{A}(x_{i})-μ_{\underline{A}}(x_{i})| dx$ для бесконечного несчетного нечеткого множества $A$ с носителем $(a; b)$ .

Квадратичный индекс нечеткости:

$d (A) = \frac{2}{\sqrt{n}} e (A, \underset{ˉ}{A})$ для конечного нечеткое множества $A$ ;
$d (A) = lim_{n \to \infty} (\frac{2}{\sqrt{n}} \sqrt{\sum_{i = 1}^{n} {(μ_{A} (x_{i}) - μ_{\underline{A}} (x_{i}))}^{2}})$ для бесконечного счетного нечеткого множества $A$ ;
$d (A) = \frac{2}{\sqrt{b - a}} \sqrt{\int_{a}^{b} {(μ_{A} (x_{i}) - μ_{\underline{A}} (x_{i}))}^{2} dx}$ для бесконечного несчетного нечеткого множества $A$ с носителем $(a; b)$ .

Линейный и квадратичный индексы нечеткости нечеткого множества $A$ можно определить, используя операцию дополнения.

Линейный индекс нечеткости с дополнением:

$d (A) = \frac{2}{n} \sum_{i = 1}^{n} min \{μ_{A} (x_{i}); μ_{\overset{ˉ}{A}} (x_{i})\}$ для конечного нечеткого множества $A$ ;
$d (A) = lim_{n \to \infty} (\frac{2}{n} \sum_{i = 1}^{n} min \{μ_{A} (x_{i}); μ_{\overset{ˉ}{A}} (x_{i})\})$ для бесконечного счетного нечеткого множества $A$ ;
$d (A) = \frac{2}{b - a} \int_{a}^{b} min \{μ_{A} (x); μ_{\overset{ˉ}{A}} (x)\} dx$ для бесконечного несчетного нечеткого множества $A$ с носителем $(a; b)$ .

Квадратичный индекс нечеткости с дополнением:

$d (A) = \frac{2}{\sqrt{n}} \sqrt{\sum_{i = 1}^{n} min \{μ_{A}^{2} (x_{i}); μ_{\overset{ˉ}{A}}^{2} (x_{i})\}}$ – для конечного нечеткое множества $A$ ;
$d (A) = lim_{n \to \infty} (\frac{2}{\sqrt{n}} \sqrt{\sum_{i = 1}^{n} min \{μ_{A}^{2} (x_{i}); μ_{\overset{ˉ}{A}}^{2} (x_{i})\}})$ – для бесконечного счетного нечеткого множества $A$ ;
$d (A) = \frac{2}{\sqrt{b - a}} \sqrt{\int_{a}^{b} min \{μ_{A}^{2} (x); μ_{\overset{ˉ}{A}}^{2} (x)\} dx}$ – для бесконечного несчетного нечеткого множества $A$ с носителем $(a; b)$ .

С ближайшим обычным множеством связаны свойства:

$\underset{ˉ}{A \cap B} = \underset{ˉ}{A} \cap \underset{ˉ}{B}$ ;
$\underset{ˉ}{A \cup B} = \underset{ˉ}{A} \cup \underset{ˉ}{B}$ ;
$\forall x \in X : |μ_{A}(x)-μ_{\underline{A}}(x)| = μ_{A \cap \overset{ˉ}{A}} (x)$ .

На основании последнего свойства линейный индекс нечеткости можно представить в следующем виде:

$d (A) = \frac{2}{n} \sum_{i = 1}^{n} ∣ μ_{A} (x_{i}) - μ_{\underline{A}} (x_{i}) ∣ = \frac{2}{n} \sum_{i = 1}^{n} μ_{A \cap \overset{ˉ}{A}} (x_{i})$ ,

откуда следует, что линейный индекс нечеткости нечеткого подмножества равен линейному индексу нечеткости дополнения этого нечеткого подмножества, т.е. $d (A) = d (\overline{A})$ . Следовательно, операции пересечения и объединения не дают эффекта увеличения или понижения нечеткости.

Векторный индикатор нечеткости – это нечеткое множество с функцией принадлежности ${2μ}_{A \cap \overset{ˉ}{A}} (x)$ .

Если система может пребывать в $N$ различных состояниях с вероятностями $p_{1}$ ... $p_{N}$ , то энтропия системы определяется как:

$H (p_{1}, \dots, p_{N}) = - \sum_{i = 1}^{N} (p_{i} ln p_{i})$ .

Энтропия минимальна $H = 0$ при достоверно известном и неизменном состоянии системы, т.е. когда для одного из состояний $p_{r} = 1$ , $1 \leq r \leq N$ , а для остальных состояний $p_{i} = 0$ , $i \neq r, i \in \{1; 2; . . .; N - 1; N\}$ . Энтропия максимальна $H = ln N$ при равновероятных состояниях системы $p_{1} = p_{2} = \dots = p_{N} = \frac{1}{N}$ . Таким образом, мерой неопределенности состояния системы может служить следующая характеристика, меняющаяся в интервале $0 \leq H \leq 1$ :

H (p_{1}, \dots, p_{N}) = - \frac{1}{ln N} \sum_{i = 1}^{N} (p_{i} ln p_{i})

Если нечеткое множество $A$ задано на конечном счетном универсальном множестве $X$ , то степень нечеткости данного нечеткого множества можно оценить через энтропию. При этом для всех $N$ элементов носителя нечеткого множества $S_{A}$ вводится частота:

$π_{A} (x_{i}) = \frac{μ_{A} (x_{i})}{\sum_{i = 1}^{N} μ_{A} (x_{i})}, i = 1 \dots N$ .

Очевидно, что $\sum_{i = 1}^{N} π_{A} (x_{i}) = 1$ . Это позволяет рассматривать введенную частоту как аналог вероятности и по аналогии посчитать энтропию нечеткости данного множества:

$H (π_{A} (x_{1}), \dots, π_{A} (x_{N})) = - \frac{1}{ln N} \sum_{i = 1}^{N} (π_{A} (x_{i}) ln (π_{A} (x_{i})))$ .