2.1. Определение и основные характеристики нечетких множеств

Нечеткое множество(fuzzyset) представляет собой совокупность элементов произвольной природы, относительно которых нельзя точно утверждать – обладают ли эти элементы некоторым характеристическим свойством, которое используется для задания нечеткого множества.

Пусть $X$ – универсальное (базовое) множество, $x$ – элемент $X$ , а $R$ – некоторое свойство. Обычное (четкое) подмножество $A$ универсального множества $X$ , элементы которого удовлетворяют свойству $R$ , определяется как множество упорядоченных пар
$A = \{μ_{A} (x) / x\}$ , где $μ_{A} (x)$ – характеристическая функция, принимающая значение $1$ , если $x$ удовлетворяет свойству $R$ , и $0$ – в противном случае.

Нечеткое подмножество отличается от обычного тем, что для элементов $x$ из $X$ нет однозначного ответа «да-нет» относительно свойства $R$ . В связи с этим, нечеткое подмножество $A$ универсального множества $X$ определяется как множество упорядоченных пар $A = \{μ_{A} (x) / x\}$ , где $μ_{A} (x)$ – характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве $M = [0; 1]$ . Функция принадлежности указывает степень (или уровень) принадлежности элемента $x$ подмножеству $A$ . Множество $M$ называют множеством принадлежностей. Если $M = \{0; 1\}$ , то нечеткое подмножество $A$ может рассматриваться как обычное или четкое множество. Степень принадлежности $μ_{A} (x)$ является субъективной мерой того, насколько элемент $x \in X$ , соответствует понятию, смысл которого формализуется нечетким множеством $A$ .

Носителем нечеткого множества $A$ является четкое подмножество $S_{A}$ универсального множества $X$ со свойством $μ_{A} (x) > 0$ , т.е. $S_{A} = \{x ∣ x \in X \land μ_{A} (x) > 0\}$ . Иными словами, носителем нечеткого множества $A$ является подмножество $S_{A}$ универсального множества $X$ , для элементов которого функция принадлежности $μ_{A} (x) > 0$ больше нуля. Иногда носитель нечеткого множества обозначают $support (A)$ .

Если носителем нечеткого множества $A$ является дискретное подмножество $S_{A}$ , то нечеткое подмножество $A$ универсального множества $X$ , состоящего из $n$ элементов, можно представить в виде объединения конечного числа одноточечных множеств $μ_{A} (x) / x$ при помощи символа $\sum$ : $A = \sum_{i = 1}^{n} μ_{A} (x_{i}) / x_{i}$ . При этом подразумевается, что элементы $x_{i}$ упорядочены по возрастанию в соответствии со своими индексами, т.е. $x_{1} < x_{2} < x_{3} < \dots < x_{n}$ .

Если носителем нечеткого множества $A$ является непрерывное подмножество $S_{A}$ , то нечеткое подмножество $A$ универсального множества $X$ , рассматривая символ $\int$ как непрерывный аналог введенного выше символа объединения для дискретных нечетких множеств $\sum$ , можно представить в виде объединения бесконечного числа одноточечных множеств $μ_{A} (x) / x$ :

$A = \int_{X} μ_{A} (x) / x$ .

Пример. Пусть универсальное множество $X$ соответствует множеству возможных значений толщин изделия от $10 мм$ до $40 мм$ с дискретным шагом $1 мм$ . Нечеткое множество $A$ , соответствующее нечеткому понятию «малая толщина изделия», может быть представлено в следующем виде:

$A = \{1 / 10; 0,9 / 11; 0,8 / 12; 0,7 / 13; 0,5 / 14; 0,3 / 15; 0,1 / 16; 0 / 17; \dots; 0 / 40\}$ ,

$A = 1 / 10 + 0,9 / 11 + 0,8 / 12 + 0,7 / 13 + 0,5 / 14 + 0,3 / 15 + 0,1 / 16 + 0 / 17 + \dots + 0 / 40$ ,

где знак суммирования обозначает не операцию арифметического сложения, а объединения элементов в одно множество. Носителем нечеткого множества $A$ будет конечное подмножество (дискретный носитель):

$S_{A} = \{10; 11; 12; 13; 14; 15; 16\}$ .

Если же универсальное множество $X$ является множеством действительных чисел от $10$ до $40$ , т.е. толщина изделия может принимать все возможные значения в этих пределах, то носителем нечеткого множества $A$ является отрезок $S_{A} = [10; 16]$ .

Нечеткое множество с дискретным носителем может быть представлено в виде отдельных точек на плоскости, нечеткое множество с непрерывным носителем может быть представлено в виде кривой, что соответствует дискретной и непрерывной функциям принадлежности $μ_{A} (x)$ , заданным на универсальном множестве $X$ (рис.2.1).

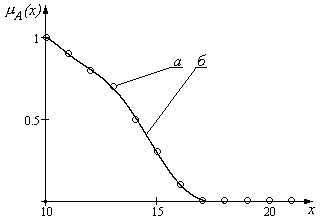
Рис.2.1. Функции принадлежности нечетких множеств с (а)-дискретным и (б)-непрерывным носителями

Пример. Пусть $X = \{0; 1; 2; \dots\}$ – множество целых неотрицательных чисел. Нечеткое множество $ital малый$ можно определить как $μ_{ital малый} (x) = {(x (1 + {(0,1 x)}^{2}))}^{- 1}$ .

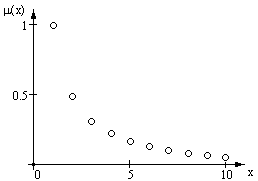
Рис.2.2. Графическое представление нечеткого множества $малый$

Нечеткое множество $A$ называется конечным, если его носитель $S_{A}$ является конечным четким множеством. При этом, по аналогии с обычными множествами, можно говорить, что такое нечеткое множество имеет конечную мощность $card (A) = card (S_{A})$ . Нечеткое множество $A$ называется бесконечным, если его носитель $S_{A}$ не является конечным четким множеством. При этом счетным нечетким множеством будет называться нечеткое множество с счетным носителем, имеющим счетную мощность в обычном смысле в терминах теории четких множеств, т.е. если $S_{A}$ содержит бесконечное число элементов, которые однако можно пронумеровать натуральными числами $1,2,3 . . .$ , причем достичь последнего элемента при нумерации принципиально невозможно. Несчетным нечетким множеством будет называться нечеткое множество со несчетным носителем, имеющим несчетную мощность континуума, т.е. если $S_{A}$ содержит бесконечное число элементов, которые невозможно пронумеровать натуральными числами $1,2,3 . . .$

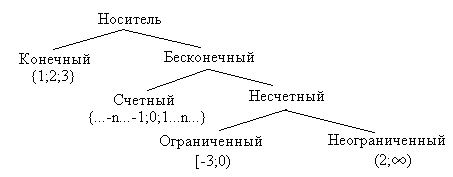
Пример. Нечеткое понятие «очень маленькое количество деталей» может быть представлено в виде конечного нечеткого множества $A = 1 / 0 + 0,9 / 1 + 0,8 / 2 + 0,7 / 3 + 0,5 / 4 + 0,1 / 5 + 0 / 6 + \dots$ с мощностью $card (A) = 6$ и носителем $S_{A} = \{0; 1; 2; 3; 4; 5\}$ , который является конечным четким множеством. Нечеткое понятие «очень большое количество деталей» может быть представлено в виде $A = 0 / 0 + \dots + 0,1 / 10 + 0,4 / 11 + 0,7 / 12 + 0,9 / 13 + 1 / 14 + 1 / 15 + \dots + 1 / n + \dots, n \in N$ – нечеткого множества с бесконечным счетным носителем $S_{A} \equiv N$ (множество натуральных чисел), который имеет счетную мощность в обычном смысле.

Пример. Несчетное нечеткое множество $A$ , соответствующее нечеткому понятию «очень горячо», задано на универсальном множестве значений температур (в Кельвинах) температурой $x \in [0; \infty)$ и функцией принадлежности $μ_{A} = 1 - e^{- x}$ , с носителем $S_{A} \equiv R_{+}$ (множество неотрицательных действительных чисел), который имеет несчетную мощность континуума.

Величина $sup_{x \in X} μ_{A} (x)$ называется высотой нечеткого множества.

Нечеткое множество $A$ нормально, если его высота равна $1$ , т.е. верхняя граница его функции принадлежности $sup_{x \in X} μ_{A} (x) = 1$ . При $sup_{x \in X} μ_{A} (x) < 1$ нечеткое множество называется субнормальным.

Нечеткое множество называется пустым, если $\forall x \in X μ_{A} (x) = 0$ .

Непустое субнормальное множество всегда можно нормализовать, разделив все значения функции принадлежности на ее максимальное значение $\frac{μ_{A} (x)}{sup_{x \in X} μ_{A} (x)}$ .

Нечеткое множество называется унимодальным, если $μ_{A} (x) = 1$ только для одной точки $x$ (моды) универсального множества $X$ .

Нечеткое множество называется точечным, если $μ_{A} (x) > 0$ только для одной точки $x$ универсального множества $X$ .

Множеством $α$ -уровня нечеткого множества $A$ , определенного на универсальном множества $X$ , называется четкое подмножество $A_{α}$ универсального множества $X$ , определяемое в виде:

$A_{α} = \{x \in X ∣ μ_{A} (x) \geq α\}$ , где $α \in [0; 1]$ .

Пример. $A = 0,8 / 1 + 0,6 / 2 + 0,2 / 3 + 1 / 4$ , $A_{0,5} = \{1; 2; 4\}$ , где $A_{0,5}$ – четкое множество, включающее те элементы $x$ упорядоченных пар $μ_{A} (x) / x$ , составляющих нечеткое множество $A$ , для которых значение функции принадлежности которых удовлетворяет условию $μ_{A} (x) \geq α$ .

Для множеств $α$ -уровня выполняется следующее свойство: если $α_{1} \geq α_{2}$ , то мощность подмножества $A_{α_{1}}$ не больше мощности подмножества $A_{α_{2}}$ .

Элементы $x \in X$ , для которых $μ_{A} (x) = 0,5$ называются точками перехода нечеткого множества $A$ .

Ядром нечеткого множества $A$ , определенного на универсальном множестве $X$ , называется четкое множество $core (A)$ , элементы которого удовлетворяют условию $core (A) = \{x \in X ∣ μ_{A} (x) = 1\}$ .

Границей нечеткого множества $A$ , определенного на универсальном множестве $X$ , называется четкое множество $front (A)$ , элементы которого удовлетворяют условию $front (A) = \{x \in X ∣ 0 < μ_{A} (x) < 1\}$ .

Пример.Пусть $X = \{0; 1; 2; \dots; 10\}$ , $M = [0; 1]$ . Нечеткое множество $несколько$ можно определить на универсальном множестве натуральных чисел следующим образом: $несколько = 0,5 / 3 + 0,8 / 4 + 1 / 5 + 1 / 6 + 0,8 / 7 + 0,5 / 8$ ; его характеристики: $высота = 1$ , $носитель = \{3; 4; 5; 6; 7; 8\}$ , $точки перехода = \{3; 8\}$ , $ядро = \{5; 6\}$ , $граница = \{3; 4; 7; 8\}$ .

Нечеткое множество $A$ , определенное на универсальном множестве $X$ , называется выпуклым, если $μ_{A} (x) \geq min \{μ_{A} (a); μ_{A} (b)\}; a < x < b; x, a, b \in X$ (рис.2.3).

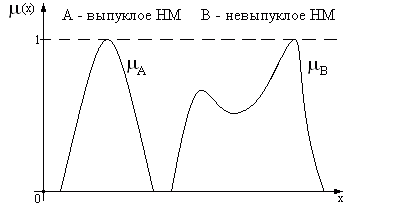
Рис.2.3. Функции принадлежности выпуклого и невыпуклого нечетких множеств