2.2. Функции принадлежности и методы их построения

Введенное определение нечеткого множества (2.1) не накладывает ограничений на выбор функции принадлежности. Однако, на практике целесообразно использовать аналитическое представление функции принадлежности $μ_{A} (x)$ нечеткого множества A с элементами $x$ , нечетко обладающими определяющим множество свойством R. Типизация функций принадлежности в контексте решаемой технической задачи существенно упрощает соответствующие аналитические и численные расчеты при применении методов теории нечетких множеств. Выделяют следующие типовые функции принадлежности [32], [33].

Треугольные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно равно», «среднее значение», «расположен в интервале», «подобен объекту», «похож на предмет» и т.п.:

треугольная и трапецеидальная функции

trimf (x,a,b,c) = \{\begin{matrix} 0, x \leq a; \\ \frac{x - a}{b - a}, a \leq x \leq b; \\ \frac{c - x}{c - b}, b \leq x \leq c; \\ 0, c \leq x; \end{matrix}

trapmf (x,a,b,c,d) = \{\begin{matrix} 0, x \leq a; \\ \frac{x - a}{b - a}, a \leq x \leq b; \\ 1, b \leq x \leq c; \\ \frac{d - x}{d - c}, c \leq x \leq d; \\ 0, d \leq x; \end{matrix}

Z-образные функции принадлежности, использующиеся для задания неопределенностей типа: «малое количество», «небольшое значение», «незначительная величина», «низкий уровень» и т.п.:

квадратичный и гармонический Z-сплайны

zm f_{1} (x,a,b) = \{\begin{matrix} 1, x \leq a; \\ 1 - 2 {(\frac{x-a}{b-a})}^{2}, a < x \leq \frac{a+b}{2}; \\ 2 {(\frac{b-x}{b-a})}^{2}, \frac{a + b}{2}<x<b; \\ 0, b \leq x; \end{matrix}

zm f_{2} (x,a,b) = \{\begin{matrix} 1, x < a; \\ \frac{1}{2} + \frac{1}{2} \cos (\frac{x-a}{b-a}); a \leq x \leq b; \\ 0, x > b; \end{matrix}

Z-сигмоидальная и Z-линейная функции

sigmf (x,a,b) = \frac{1}{1 + \exp (-a(x-b))}, a < 0;

zlinemf (x,c,d) = \{\begin{matrix} 1, - \infty < x \leq c; \\ \frac{d - x}{b - c}, c < x \leq d; \\ 0, x > d; \end{matrix}

S-образные функции принадлежности, использующиеся для задания неопределенностей типа: «большое количество», «большое значение», «значительная величина», «высокий уровень» и т.п.:

квадратичный и гармонический S-сплайны

sm f_{1} (x,a,b) = \{\begin{matrix} 0, x \leq a; \\ 2 {(\frac{x-a}{b-a})}^{2}, a < x \leq \frac{a + b}{2}; \\ 1 - 2 {(\frac{b-x}{b-a})}^{2}, \frac{a + b}{2}<x<b; \\ 1, b \leq x; \end{matrix}

sm f_{2} (x,a,b) = \{\begin{matrix} 0, x < a; \\ \frac{1}{2} + \frac{1}{2} \cos (\frac{x-b}{b-a}); a \leq x \leq b; \\ 1, x > b; \end{matrix}

S-сигмоидальная и S-линейная функции

sigmf (x,a,b) = \frac{1}{1 + \exp (-a(x-b))}, a > 0;

slinemf (x,a,b) = \{\begin{matrix} 0, x \leq a; \\ \frac{x - a}{b - a}, a < x \leq b; \\ 1, x > b; \end{matrix}

П-образные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно в пределах от и до», «примерно равно», «около» и т.п.:

колоколообразная и гауссова функции

gbellmf (x,a,b,c) = \frac{1}{1 + {|\frac{x - c}{a}|}^{2b}};

gaussmf (x,σ,c) = \exp (-\frac{{(x-c)}^{2}}{{2σ}^{2}})

Существует множество других функций принадлежности нечетких множеств, заданных как композиции вышеупомянутых базовых функций (двойная гауссова, двойная сигмоидальная и т.п.), либо как комбинации по участкам возрастания и убывания (сигмоидально-гауссова, сплайн-треугольная и т.п.).

Функция принадлежности $μ_{A} (x)$ – это некоторая не вероятностная субъективная мера нечеткости, определяемая в результате опроса экспертов о степени соответствия элемента x понятию, формализуемому нечетким множеством A . В отличие от вероятностной меры, которая является оценкой стохастической неопределенности, имеющей дело с неоднозначностью наступления некоторого события в различные моменты времени, нечеткая мера является численной оценкой лингвистической неопределенности, связанной с неоднозначностью и расплывчатостью категорий человеческого мышления. При построении функции принадлежности $μ_{A} (x)$ с каждым нечетким множеством A ассоциируется некоторое свойство, признак или атрибут R , который характеризует некоторую совокупность объектов X . Чем в большей степени конкретный объект $x ∈ X$ обладает этим свойством R , тем более близко к соответствующее значение $μ_{A} (x)$ . Если элемент $x ∈ X$ определенно обладает этим свойством R , то $μ_{A} (x)= 1$ , если же $x ∈ X$ определенно не обладает этим свойством R , то $μ_{A} (x)= 0$ . Существуют прямые и косвенные методы построения функций принадлежности [18]-[20].

Прямые методы (наиболее известны методы относительных частот, параметрический, интервальный) целесообразно использовать для измеримых свойств, признаков и атрибутов, таких как скорость, время, температура, давление и т.п. При использовании прямых методов зачастую не требуется абсолютно точного поточечного задания $μ_{A} (x)$ . Как правило, бывает достаточно зафиксировать вид функции принадлежности и характерные точки, по которым дискретное представление функции принадлежности аппроксимируется непрерывным аналогом – наиболее подходящей типовой функцией принадлежности.

Косвенные методы (наиболее известен метод парных сравнений) используются в тех случаях, когда отсутствуют измеримые свойства объектов в рассматриваемой предметной области. В силу специфики рассматриваемых задач при построении нечетких систем автоматического управления, как правило, применяются прямые методы. В свою очередь, в зависимости от числа привлеченных к опросу экспертов как прямые, так и косвенные методы делятся на одиночные и групповые. Наиболее грубую оценку характеристических точек функции принадлежности можно получить путем опроса одного эксперта, который просто задает для каждого значения $x ∈ X$ соответствующее значение $μ_{A} (x)$ .

Пример. Рассмотрим нечеткое множество A , соответствующее понятию «расход теплоносителя небольшой». Объект x – расход теплоносителя, X $(0;x_{\max})$ – множество физически возможных значений скорости изменения температуры. Эксперту предъявляются различные значения расхода теплоносителя x и задается вопрос: с какой степенью уверенности 0 ≤ $μ_{A} (x)$ ≤ 1 эксперт считает, что данный расход теплоносителя x небольшой. При $μ_{A} (x)= 0$ – эксперт абсолютно уверен, что расход теплоносителя x небольшой. При $μ_{A} (x)= 1$ – эксперт абсолютно уверен, что расход теплоносителя x нельзя классифицировать как небольшой.

Метод относительных частот. Пусть имеется m экспертов, $n_{1}$ из которых на вопрос о принадлежности элемента $x ∈ X$ нечеткому множеству A отвечают положительно. Другая часть экспертов $n_{2} = m - n_{1}$ отвечает на этот вопрос отрицательно. Тогда принимается $μ_{A} (x) = \frac{n_{1}}{n_{1}+n_{2}} = \frac{n_{1}}{m}$ .

Пример. Рассмотрим нечеткое множество A , соответствующее понятию «скорость изменения температуры положительная средняя». Объект x – скорость изменения температуры, X $({-x}_{\max};x_{\max})$ – множество физически возможных значений скорости изменения температуры. Экспертам предъявляются различные значения скорости изменения температуры x и каждому из них задается вопрос: считает ли эксперт, что данная скорость изменения температуры x положительная средняя. Результаты опроса сведены в табл.2.1.

Табл.2.1

Для непрерывного представления нечеткой переменной используем какую нибудь из П-образных функций принадлежности, например, Гауссову. Из множества гауссовых функций $gaussmf (x,σ,c) = \exp (-\frac{{(x - c)}^{2}}{{2 σ}^{2}})$ через характерные точки функции принадлежности: точку перехода $μ_{A} (3) = 0,5$ и максимум $μ_{A} (5) = 1$ ; проходит функция с параметрами σ = 1,7 , c = 5 . В качестве альтернативного метода перехода от дискретного ряда точек к непрерывному заданию функции принадлежности можно предложить поиск параметров Гауссовой функции принадлежности, максимально близко аппроксимирующей дискретный ряд по критерию СКО (рис.2.4).

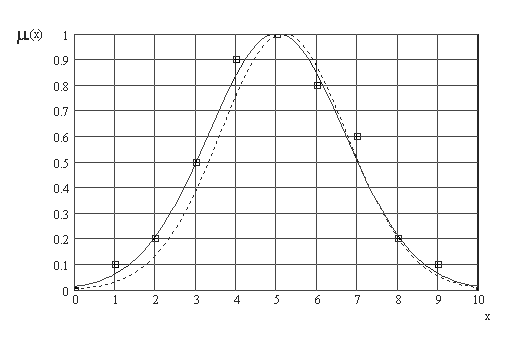
Рис.2.4. Аппроксимация дискретного ряда () непрерывной Гауссовой функцией принадлежности ( – по характерным точкам, – – по СКО)