2.3. Операции над нечеткими множествами

Включение. Пусть $A$ и $B$ – нечеткие множества на универсальном множестве $X$ . Говорят, что $A$ содержится в $B$ , или $B$ включает $A$ , т.е. $A \subset B$ , если $\forall x \in X μ_{A} (x) \leq μ_{B} (x)$ . Иногда используют термин «доминирование», т.е. $B$ доминирует $A$ при $A \subset B$ .

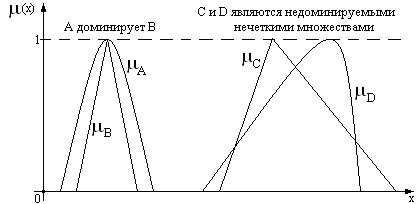
Рис.2.5. Включение (доминирование) нечетких множеств

Равенство. Пусть $A$ и $B$ – нечеткие множества на универсальном множестве $X$ . Говорят, что $A$ и $B$ равны, т.е. $A = B$ , если $\forall x \in X μ_{A} (x) = μ_{B} (x)$ . В противном случае $A \neq B$ .

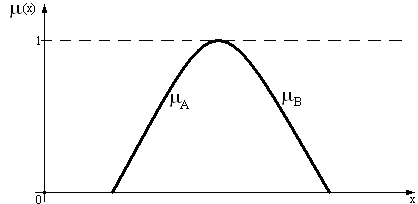
Рис.2.6. Равенство нечетких множеств

Дополнение. Пусть $A$ и $B$ – нечеткие множества с множеством принадлежностей характеристических функций $M = [0; 1]$ , заданные на универсальном множестве $X$ . Говорят, что $A$ и $B$ дополняют друг друга, т.е. $A = \overline{B}$ или $B = \overline{A}$ , если $\forall x \in X μ_{A} (x) = 1 - μ_{B} (x)$ . Очевидно следствие $\overline{A} = A$ – так называемое свойство инволюции.

Рис.2.7. Дополнение нечетких множеств

Пересечение нечетких множеств $A$ и $B$ , заданных на универсальном множестве $X$ , – это наибольшее нечеткое множество $A \cap B$ , содержащееся одновременно и в $A$ , и в $B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A \cap B} (x) = min \{μ_{A} (x); μ_{B} (x)\}$ .

Рис.2.8. Пересечение нечетких множеств

Рис.2.9. Объединение нечетких множеств

Объединение нечетких множеств $A$ и $B$ , заданных на универсальном множестве $X$ , – это наименьшее нечеткое множество $A \cup B$ , включающее как $A$ , так и $B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A \cup B} (x) = max \{μ_{A} (x); μ_{B} (x)\}$ .

Разность нечетких множеств $A$ и $B$ , заданных на универсальном множестве $X$ , – это нечеткое множество $A ∖ B = A \cap \overline{B}$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A ∖ B} (x) = μ_{A \cap \overline{B}} (x) = min \{μ_{A} (x); 1 - μ_{B} (x)\}$ .

Рис.2.10. Разность нечетких множеств

Симметрическая разность нечетких множеств $A$ и $B$ , заданных на универсальном множестве $X$ , – это нечеткое множество $A - B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A-B} (x) = |μ_{A}(x)-μ_{B}(x)|$ .

Рис.2.11. Симметрическая разность и дизъюнктивная сумма нечетких множеств

Дизъюнктивная сумма нечетких множеств $A$ и $B$ , заданных на универсальном множестве $X$ , – это нечеткое множество $A \oplus B = (A ∖ B) \cup (B ∖ A) = (A \cap \overline{B}) \cup (\overline{A} \cap B)$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A \oplus B} (x) = max \{min \{μ_{A} (x); 1 - μ_{B} (x)\};min \{1 - μ_{A} (x); μ_{B} (x)\}\}$ .

Пример.Пусть на универсальном множестве $X$ заданы следующие нечеткие подмножества:

$A = 0,4 / x_{1} + 0,2 / x_{2} + 0 / x_{3} + 1 / x_{4}$ ,

$B = 0,7 / x_{1} + 0,9 / x_{2} + 0,1 / x_{3} + 1 / x_{4}$ ,

$C = 0,1 / x_{1} + 0,1 / x_{2} + 0,2 / x_{3} + 0,9 / x_{4}$ .

В данном случае имеем следующие результаты операций.

Включение: $A \subset B$ , т.е. $A$ содержится в $B$ или $B$ доминирует $A$ , поскольку для всех элементов множеств $A, B$ выполняется условие доминирования $B$ над $A$ , $μ_{A} (x) \leq μ_{B} (x)$ . Пары $\{A; C\}$ и $\{B; C\}$ представляют пары недоминируемых нечетких множеств, так как условие доминирования не выполняются для элемента $x_{3}$ .

Равенство: $A \neq B \neq C$ . Нечеткие множества неравны, так как для не выполняются условия равенства: $\forall x \in X μ_{A} (x) = μ_{B} (x)$ , что аналогично $μ_{A} (x_{i}) = μ_{B} (x_{i}), i = 1,2,3,4$ ; $\forall x \in X μ_{A} (x) = μ_{C} (x)$ , что аналогично $μ_{A} (x_{i}) = μ_{C} (x_{i}), i = 1,2,3,4$ ; $\forall x \in X μ_{B} (x) = μ_{C} (x)$ , что аналогично $μ_{B} (x_{i}) = μ_{C} (x_{i}), i = 1,2,3,4$ .

Дополнение:

$\overline{A} = 0,6 / x_{1} + 0,8 / x_{2} + 1 / x_{3} + 0 / x_{4}$ ,

где элементы $\overline{A}$ определяются как $μ_{\overline{A}} (x_{i}) = 1 - μ_{A} (x_{i})$ ,

$\overline{B} = 0,3 / x_{1} + 0,1 / x_{2} + 0,9 / x_{3} + 0 / x_{4}$ ,

где элементы $\overline{B}$ определяются как $μ_{\overline{B}} (x_{i}) = 1 - μ_{B} (x_{i})$ ,

$\overline{C} = 0,9 / x_{1} + 0,9 / x_{2} + 0,8 / x_{3} + 0,1 / x_{4}$ ,

где элементы $\overline{C}$ определяются как $μ_{\overline{C}} (x_{i}) = 1 - μ_{C} (x_{i})$ .

Пересечение:

$A \cap B = 0,4 / x_{1} + 0,2 / x_{2} + 0 / x_{3} + 1 / x_{4}$ ,

где элементы нечеткого множества $A \cap B$ определяются как:

$μ_{A \cap B} (x_{1}) = min \{μ_{A} (x_{1}); μ_{B} (x_{1})\} = min \{0,4; 0,7\} = 0,4$ ,

$μ_{A \cap B} (x_{2}) = min \{μ_{A} (x_{2}); μ_{B} (x_{2})\} = min \{0,2; 0,9\} = 0,2$ ,

$μ_{A \cap B} (x_{3}) = min \{μ_{A} (x_{3}); μ_{B} (x_{3})\} = min \{0; 0,1\} = 0$ ,

$μ_{A \cap B} (x_{4}) = min \{μ_{A} (x_{4}); μ_{B} (x_{4})\} = min \{1; 1\} = 1$ .

Аналогично определяются нечеткие множества $B \cap C$ и $A \cap C$ :

$B \cap C = 0,1 / x_{1} + 0,1 / x_{2} + 0,1 / x_{3} + 0,9 / x_{4}$ ,

$A \cap C = 0,1 / x_{1} + 0,1 / x_{2} + 0,2 / x_{3} + 0,9 / x_{4}$ .

Объединение:

$A \cup B = 0,7 / x_{1} + 0,9 / x_{2} + 0,1 / x_{3} + 1 / x_{4}$ ,

где элементы нечеткого множества $A \cup B$ определяются как:

$μ_{A \cup B} (x_{1}) = max \{μ_{A} (x_{1}); μ_{B} (x_{1})\} = max \{0,4; 0,7\} = 0,7$ ,

$μ_{A \cup B} (x_{2}) = max \{μ_{A} (x_{2}); μ_{B} (x_{2})\} = max \{0,2; 0,9\} = 0,9$ ,

$μ_{A \cup B} (x_{3}) = max \{μ_{A} (x_{3}); μ_{B} (x_{3})\} = max \{0; 0,1\} = 0,1$ ,

$μ_{A \cup B} (x_{4}) = max \{μ_{A} (x_{4}); μ_{B} (x_{4})\} = max \{1; 1\} = 1$ .

Аналогично определяются нечеткие множества $B \cup C$ и $A \cup C$ :

$B \cup C = 0,7 / x_{1} + 0,9 / x_{2} + 0,2 / x_{3} + 1 / x_{4}$ ,

$A \cup C = 0,4 / x_{1} + 0,2 / x_{2} + 0,2 / x_{3} + 1 / x_{4}$ .

Разность:

$A ∖ B = A \cap \overline{B} = 0,3 / x_{1} + 0,1 / x_{2} + 0 / x_{3} + 0 / x_{4}$ ,

где элементы нечеткого множества $A ∖ B$ определяются как:

$μ_{A / B} (x_{1}) = μ_{A \cap \bar{B}} (x_{1}) = min \{μ_{A} (x_{1}); μ_{\overline{B}} (x_{1})\} = min \{0,4; 0,3\} = 0,3$ ,

$μ_{A ∖ B} (x_{2}) = μ_{A \cap \bar{B}} (x_{2}) = min \{μ_{A} (x_{2}); μ_{\overline{B}} (x_{2})\} = min \{0,2; 0,1\} = 0,1$ ,

$μ_{A ∖ B} (x_{3}) = μ_{A \cap \bar{B}} (x_{3}) = min \{μ_{A} (x_{3}); μ_{\overline{B}} (x_{3})\} = min \{0; 0,9\} = 0$ ,

$μ_{A ∖ B} (x_{4}) = μ_{A \cap \bar{B}} (x_{4}) = min \{μ_{A} (x_{4}); μ_{\overline{B}} (x_{4})\} = min \{1; 0\} = 0$ .

Аналогичным образом определяется нечеткое множество $B / A$ :

$B ∖ A = B \cap \overline{A} = 0,6 / x_{1} + 0,8 / x_{2} + 0,1 / x_{3} + 0 / x_{4}$ .

Симметрическая разность:

$A - B = 0,3 / x_{1} + 0,7 / x_{2} + 0,1 / x_{3} + 0 / x_{4}$ ,

где элементы нечеткого множества $A - B$ определяются как:

$μ_{A - B} (x_{1}) = |μ_{A}(x_{1})-μ_{B}(x_{1})| = |0,4-0,7| = 0,3$ ,

$μ_{A - B} (x_{2}) = |μ_{A}(x_{2})-μ_{B}(x_{2})| = |0,2-0,9| = 0,7$ ,

$μ_{A - B} (x_{3}) = |μ_{A}(x_{3})-μ_{B}(x_{3})| = |0-0,1| = 0,1$ ,

$μ_{A - B} (x_{4}) = |μ_{A}(x_{4})-μ_{B}(x_{4})| = |1-1| = 0$ .

Дизъюнктивная сумма:

$A \oplus B = 0,6 / x_{1} + 0,8 / x_{2} + 0,1 / x_{3} + 0 / x_{4}$ ,

где элементы нечеткого множества $A \oplus B$ определяются как:

$μ_{A \oplus B} (x_{1}) = max \{min \{μ_{A} (x_{1}); 1 - μ_{B} (x_{1})\};min \{1 - μ_{A} (x_{1}); μ_{B} (x_{1})\}\} = max \{min \{0,4; 1 - 0,7\};min \{1 - 0,4; 0,7\}\} = max \{min \{0,4; 0,3\};min \{0,6; 0,7\}\} = max \{0,3; 0,6\} = 0,6$ ,

$μ_{A \oplus B} (x_{2}) = max \{min \{μ_{A} (x_{2}); 1 - μ_{B} (x_{2})\};min \{1 - μ_{A} (x_{2}); μ_{B} (x_{2})\}\} = max \{min \{0,2; 1 - 0,9\};min \{1 - 0,2; 0,9\}\} = max \{min \{0,2; 0,1\};min \{0,8; 0,9\}\} = max \{0,1; 0,8\} = 0,8$ ,

$μ_{A \oplus B} (x_{3}) = max \{min \{μ_{A} (x_{3}); 1 - μ_{B} (x_{3})\};min \{1 - μ_{A} (x_{3}); μ_{B} (x_{3})\}\} = max \{min \{0; 1 - 0,1\};min \{1 - 0; 0,1\}\} max \{min \{0; 0,9\};min \{1; 0,1\}\} = max \{0; 0,1\} = 0,1$ ,

$μ_{A \oplus B} (x_{4}) = max \{min \{μ_{A} (x_{4}); 1 - μ_{B} (x_{4})\};min \{1 - μ_{A} (x_{4}); μ_{B} (x_{4})\}\} = max \{min \{1; 1 - 1\};min \{1 - 1; 1\}\} = max \{min \{1; 0\};min \{0; 1\}\} = max \{0; 0\} = 0$ .

Пусть $A$ , $B$ и $C$ – нечеткие множества, заданные на универсальном множестве $X$ . Тогда для операций пересечения и объединения нечетких множеств выполняются следующие свойства:

$\{\begin{matrix} A \cap B = B \cap A, \\ A \cup B = B \cup A, \end{matrix}$ – коммутативность;
$\{\begin{matrix} (A \cap B) \cap C = A \cap (B \cap C), \\ (A \cup B) \cup C = A \cup (B \cup C), \end{matrix}$ – ассоциативность;
$\{\begin{matrix} A \cap (B \cup C) = (A \cap B) \cup (A \cap C), \\ A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \end{matrix}$ – дистрибутивность;
$\{\begin{matrix} A \cap A = A, \\ A \cup A = A, \end{matrix}$ – идемпотентность;
$A \cup \emptyset = A$ , где $\emptyset$ – пустое множество, т.е. $μ_{\emptyset} (x) = 0$ , $\forall x \in X$ .
$A \cap \emptyset = \emptyset$ ;
$A \cap X = A$ ;
$A \cup X = X$ ;
$\{\begin{matrix} \overset{_______}{A \cap B} = \overline{A} \cup \overline{B}, \\ \overset{_______}{A \cup B} = \overline{A} \cap \overline{B}, \end{matrix}$ – теоремы Де Моргана.
$\{\begin{matrix} A \cap \overline{A} \neq \emptyset, \\ A \cup \overline{A} \neq X, \end{matrix}$ – в отличие от аналогичных свойств для обычного (четкого) множества, заданного на множестве $E$ подмножества $D$ , для которого $\{\begin{matrix} D \cap \overline{D} = \emptyset, \\ D \cup \overline{D} = E, \end{matrix}$
$A \oplus B = (A ∖ B) \cup (B ∖ A)$ .

Введенные выше операции над нечеткими множествами основаны на использовании операций $max$ и $min$ . В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им лингвистических связок естественного языка «и», «или», «не» [7]. Один из подходов к операторам пересечения и объединения заключается в их определении при помощи нечетких операторов, т.н.треугольных норм и конорм. Следует обратить внимание на то, что представленные выше операции пересечения $min \{μ_{A} (x), μ_{B} (x)\}$ и объединения $max \{μ_{A} (x), μ_{B} (x)\}$ , использующиеся как самостоятельно, так и при введении операций разности, симметрической разности и дизъюнктивной суммы – это только один из возможных вариантов определения данных операций, веденный основоположником теории нечетких множеств Л.Заде.

Треугольной нормой ( $t$ -нормой) называется двуместная действительная функция $T$ , отображающая две функции принадлежности нормальных нечетких множеств $μ_{A} (x)$ , $μ_{B} (x)$ в одну функцию принадлежности нормального нечеткого множества и удовлетворяющая следующим условиям:

$T (0,0) = 0$ , $T (μ_{A} (x),1) = μ_{A} (x)$ , $T (1, μ_{A} (x)) = μ_{A} (x)$ – ограниченность;
$T (μ_{A} (x), μ_{B} (x)) \leq T (μ_{C} (x), μ_{D} (x))$ , если $μ_{A} (x) \leq μ_{C} (x)$ , $μ_{B} (x) \leq μ_{D} (x)$ для $\forall x \in X$ – монотонность;
$T (μ_{A} (x), μ_{B} (x)) = T (μ_{B} (x), μ_{A} (x))$ – коммутативность;
$T (μ_{A} (x), T (μ_{B} (x), μ_{C} (x))) = T (T (μ_{A} (x), μ_{B} (x)), μ_{C} (x))$ – ассоциативность.

Примерами $t$ -норм являются следующие функции:

$min \{μ_{A} (x), μ_{B} (x)\}$ – нечеткое «И» по Заде,

$max \{0; μ_{A} (x) + μ_{B} (x) - 1\}$ – нечеткое «И» по Лукашевичу,

$μ_{A} (x) \cdot μ_{B} (x)$ – нечеткое «И» по Бандлеру.

Треугольной конормой ( $t$ -конормой) называется двуместная действительная функция $T$ , отображающая две функции принадлежности нормальных нечетких множеств $μ_{A} (x)$ , $μ_{B} (x)$ в одну функцию принадлежности нормального нечеткого множества и удовлетворяющая следующим условиям:

$T (1,1) = 1$ , $T (μ_{A} (x),0) = μ_{A} (x)$ , $T (0, μ_{A} (x)) = μ_{A} (x)$ – ограниченность;
$T (μ_{A} (x), μ_{B} (x)) \geq T (μ_{C} (x), μ_{D} (x))$ , если $μ_{A} (x) \leq μ_{C} (x)$ , $μ_{B} (x) \geq μ_{D} (x)$ для $\forall x \in X$ – монотонность;
$T (μ_{A} (x), μ_{B} (x)) = T (μ_{B} (x), μ_{A} (x))$ – коммутативность;
$T (μ_{A} (x), T (μ_{B} (x), μ_{C} (x))) = T (T (μ_{A} (x), μ_{B} (x)), μ_{C} (x))$ – ассоциативность.

Примерами $t$ -конорм являются следующие функции:

$max \{μ_{A} (x), μ_{B} (x)\}$ – нечеткое «ИЛИ» по Заде,

$min \{1; μ_{A} (x) + μ_{B} (x) - 1\}$ – нечеткое «ИЛИ» по Лукашевичу,

$μ_{A} (x) + μ_{B} (x) - μ_{A} (x) \cdot μ_{B} (x)$ – нечеткое «ИЛИ» по Бандлеру.

Граничное пересечение нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $A ° B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A ° B} (x) = max \{0; μ_{A} (x) + μ_{B} (x) - 1\}$ .

Граничное объединение нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $A \otimes B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A \otimes B} (x) = min \{μ_{A} (x) \cdot μ_{B} (x); 1\}$ .

Драстическое пересечение нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $AΔB$ с функцией принадлежности, заданной следующим образом:

\forall x \in X μ_{AΔB} (x) = \{\begin{matrix} μ_{B} (x), если μ_{A} (x) = 1, \\ μ_{A} (x), если μ_{B} (x) = 1, \\ 0, в остальных случаях . \end{matrix}

Драстическое объединение нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $A \nabla B$ с функцией принадлежности, заданной следующим образом:

\forall x \in X μ_{A \nabla B} (x) = \{\begin{matrix} μ_{B} (x), если μ_{A} (x) = 0, \\ μ_{A} (x), если μ_{B} (x) = 0, \\ 1, в остальных случаях . \end{matrix}

$λ$ -сумма нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество ${(A + B)}_{λ}$ с функцией принадлежности, заданной как:

$\forall x \in X μ_{{(A + B)}_{λ}} (x) = {λμ}_{A} (x) + (1 - λ) μ_{B} (x), λ \in [0; 1]$ .

Алгебраическое произведение нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $A \cdot B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A \cdot B} (x) = μ_{A} (x) \cdot μ_{B} (x)$ .

Алгебраическая сумма нечетких множеств $A$ и $B$ на универсальном множестве $X$ – это нечеткое множество $A + B$ с функцией принадлежности, заданной следующим образом:

$\forall x \in X μ_{A + B} (x) = μ_{A} (x) + μ_{B} (x) - μ_{A} (x) \cdot μ_{B} (x)$ .

Пусть $A$ , $B$ и $C$ – нечеткие множества, заданные на универсальном множестве $X$ . Тогда для операций алгебраического произведения и алгебраической суммы нечетких множеств выполняются следующие свойства:

$\{\begin{matrix} A \cdot B = B \cdot A, \\ A + B = B + A, \end{matrix}$ – коммутативность;
$\{\begin{matrix} (A \cdot B) \cdot C = A \cdot (B \cdot C), \\ (A + B) + C = A + (B + C), \end{matrix}$ – ассоциативность;
$A + \emptyset = A$ ;
$A \cdot \emptyset = \emptyset$ ;
$A \cdot X = A$ ;
$A + X = X$ ;
$\{\begin{matrix} \overset{______}{A \cdot B} = \overline{A} + \overline{B}, \\ \overset{______}{A + B} = \overline{A} \cdot \overline{B}, \end{matrix}$ – теоремы Де Моргана.
$\{\begin{matrix} A \cdot (B + C) \neq (A \cdot B) + (A \cdot C), \\ A + (B \cdot C) \neq (A + B) \cdot (A + C), \end{matrix}$ – не выполняется дистрибутивность;
$\{\begin{matrix} A \cdot A \neq A, \\ A + A \neq A, \end{matrix}$ – не выполняется идемпотентность;
$\{\begin{matrix} A \cdot \overline{A} \neq \emptyset, \\ A + \overline{A} \neq X, \end{matrix}$ – в отличие от аналогичных свойств для обычного (четкого) множества, заданного на универсальном множестве $E$ подмножества $D$ , для которого $\{\begin{matrix} D \cap \overline{D} = \emptyset, \\ D \cup \overline{D} = E . \end{matrix}$

Пусть $A$ , $B$ и $C$ – нечеткие множества, заданные на универсальном множестве $X$ . Тогда при совместном использовании операций пересечения, объединения, алгебраического произведения и алгебраической суммы нечетких множеств выполняются следующие свойства:

Доказательства приводимых свойств операций над нечеткими множествами подробно рассмотрены в [25].

Пример. Докажем теорему Де Моргана для алгебраического произведения нечетких множеств $\overset{______}{A \cdot B} = \overline{A} + \overline{B}$ . Обозначим $μ_{A} (x) = a$ , $μ_{B} (x) = b$ . Тогда в левой части равенства для функции принадлежности $μ_{\overset{___}{A \cdot B}} (x)$ каждого элемента $x$ имеем $μ_{\overset{___}{A \cdot B}} (x) = 1 - ab$ . В правой части равенства для $μ_{\bar{A} + \bar{B}} (x)$ каждого элемента $x$ имеем $μ_{\bar{A} + \bar{B}} (x) = (1 - a) + (1 - b) - (1 - a) (1 - b) = 1 - a + 1 - b - 1 + b + a - ab = 1 - ab$ . Следовательно равенство верно.

На основе операции алгебраического произведения определяется операция возведения в степень $α$ нечеткого множества $A$ , определенного на универсальном множестве $X$ , где $α$ - положительное число. Нечеткое множество $A^{α}$ определяется как:

$\forall x \in X μ_{A^{α}} (x) = μ_{A}^{α} (x)$ .

Частным случаем возведения в степень являются операции концентрации $CON (A) = A^{2}$ , которая снижает степень нечеткости описания, и растяжения $DIL (A) = A^{0,5}$ , которая повышает степень нечеткости описания (рис.2.12).

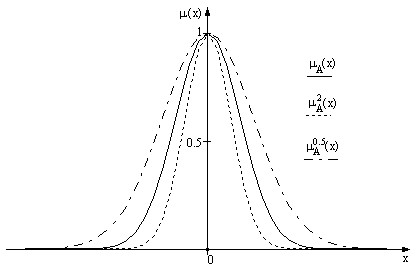
Рис.2.12. Изменение степени нечеткости описания

Умножение на число. Если $α$ – положительное число, такое, что $α \cdot max_{x \in X} \{μ_{A} (x)\} \leq 1$ , то нечеткое множество $αA$ определяется как:

$\forall x \in X μ_{αA} (x) = {αμ}_{A} (x)$ .

Выпуклая комбинация нечетких множеств.Пусть $A_{1} \dots A_{n}$ – нечеткие множества универсальных множеств $X_{1} \dots X_{n}$ соответственно, а $ω_{1} \dots ω_{n}$ – неотрицательные числа, такие, что $\sum_{i = 1}^{n} ω_{i} = 1$ . Выпуклой комбинацией нечетких множеств $A_{1} \dots A_{n}$ называется нечеткое подмножество $A$ множества $X = X_{1} \times \dots \times X_{n}$ с $n$ -мерной функцией принадлежности:

$\forall x_{i} \in X_{i} μ_{A} (x_{1}, \dots, x_{n}) = ω_{1} μ_{A_{1}} (x_{1}) + \dots + ω_{n} μ_{A_{n}} (x_{n}) = \sum_{i = 1}^{n} ω_{i} μ_{A_{i}} (x_{i})$ .

Пример. $A_{1} = 0,5 / 1 + 1 / 2$ , $A_{2} = 0,2 / 2 + 1 / 3$ , $ω_{1} = 0,4$ , $ω_{2} = 0,6$ .

A = \sum_{i} ω_{i} μ_{A_{i}} (x_{i}) = (0,5 \cdot 0,4 + 0,2 \cdot 0,6) / (1; 2) + (0,5 \cdot 0,4 + 1 \cdot 0,6) / (1; 3) + (1 \cdot 0,4 + 0,2 \cdot 0,6) / (2; 2) + (1 \cdot 0,4 + 1 \cdot 0,6) / (2; 3) = 0, 32 / (1; 2) + 0,8 / (1; 3) + 0, 52 / (2; 2) + 1 / (2; 3)

Декартово произведение нечетких множеств. Пусть $A_{1} \dots A_{n}$ – нечеткие подмножества универсальных множеств $X_{1} \dots X_{n}$ соответственно. Декартово произведение $A = A_{1} \times \dots \times A_{n}$ является нечетким подмножеством множества $X = X_{1} \times \dots \times X_{n}$ с $n$ -мерной функцией принадлежности:

$\forall x_{i} \in X_{i} μ_{A} (x_{1}, \dots, x_{n}) = min \{μ_{A_{1}} (x_{1}); \dots; μ_{A_{n}} (x_{n})\}$ .

Пример. $A_{1} = 0,3 / 1 + 1 / 2$ , $A_{2} = 0,1 / 2 + 1 / 3 + 0,2 / 4$ .

A_{1} \times A_{2} = min \{μ_{A_{1}} (1); μ_{A_{2}} (2)\} / (1; 2) + min \{μ_{A_{1}} (1); μ_{A_{2}} (3)\} / (1; 3) + min \{μ_{A_{1}} (1); μ_{A_{2}} (4)\} / (1; 4) + min \{μ_{A_{1}} (2); μ_{A_{2}} (2)\} / (2; 2) + min \{μ_{A_{1}} (2); μ_{A_{2}} (3)\} / (2; 3) + min \{μ_{A_{1}} (2); μ_{A_{2}} (4)\} / (2; 4) = min \{0,3; 0,1\} / (1; 2) + min \{0,3; 1\} / (1; 3) + min \{0,3; 0,2\} / (1; 4) + min \{1; 0,1\} / (2; 2) + min \{1; 1\} / (2; 3) + min \{1; 0,2\} / (2; 4) = 0,1 / (1; 2) + 0,3 / (1; 3) + 0,2 / (1; 4) + 0,1 / (2; 2) + 1 / (2; 3) + 0,2 / (2; 4)

Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества. Пусть $A$ – нечеткое множество, определенное на универсальном множестве $X$ и для всех $x \in X$ на этом же универсальном множестве $X$ определены нечеткие множества $K (x)$ . Совокупность всех $K (x)$ называется ядром оператора $Φ$ увеличения нечеткости. Результатом действия оператора $Φ$ на нечеткое множество $A$ является нечеткое множество вида:

$Φ (A, K) = \underset{x \in X}{\cup} (μ_{A} (x) K (x))$ ,

где $μ_{A} (x) K (x)$ – произведение числа $μ (x)$ на соответствующее нечеткое множество $K (x)$ для каждого $x \in X$ .

Пример. $X = \{1; 2; 3; 4\}$ , $A = 0,8 / 1 + 0,6 / 2 + 0,2 / 3 + 0 / 4$ , $K (1) = 1 / 1 + 0,4 / 2$ , $K (2) = 1 / 2 + 0,4 / 3 + 0,4 / 4$ , $K (3) = 1 / 3 + 0,5 / 4$ , $K (4) = 1 / 4$ .

Φ (A, K) = μ_{A} (1) K (1) \cup μ_{A} (2) K (2) \cup μ_{A} (3) K (3) \cup μ_{8} A (4) K (4) = 0,8 (1 / 1 + 0,4 / 2) \cup 0,6 (1 / 2 + 0,4 / 3 + 0,4 / 4) \cup 0,2 (1 / 3 + 0,5 / 4) \cup 0 (1 / 4) = (0,8 / 1 + 0, 32 / 2) \cup (0,6 / 2 + 0, 24 / 3 + 0, 24 / 4) \cup (0,2 / 3 + 0,1 / 4) \cup (0 / 4) = (0,8 / 1 + 0, 32 / 2 + 0 / 3 + 0 / 4) \cup (0 / 1 + 0,6 / 2 + 0, 24 / 3 + 0, 24 / 4) \cup (0 / 1 + 0 / 2 + 0,2 / 3 + 0,1 / 4) \cup (0 / 1 + 0 / 2 + 0 / 3 + 0 / 4) = max \{0,8; 0; 0; 0\} / 1 + max \{0, 32; 0,6; 0; 0\} / 2 + max \{0; 0, 24; 0,2; 0\} / 3 + max \{0; 0, 24; 0,1; 0\} / 4 = 0,8 / 1 + 0,6 / 2 + 0, 24 / 3 + 0, 24 / 4

Множеством $α$ -уровня нечеткого множества $A$ , определенного на универсальном множестве $X$ , называется четкое подмножество $A_{α}$ универсального множества $X$ , определяемое в виде:

$A_{α} = \{x \in X ∣ μ_{A} (x) \geq α\}$ , где $α \in [0; 1]$ .

Пример. $A = 0,8 / 1 + 0,6 / 2 + 0,2 / 3 + 1 / 4$ , $A_{0,5} = \{1; 2; 4\}$ , член $0,2 / 3$ в множество $A_{0,5}$ не входит, так как значение его функции принадлежности не удовлетворяет множеству уровня $α = 0,5$ .

Для множеств $α$ -уровня выполняется следующее свойство: если $α_{1} \geq α_{2}$ , то $A_{α_{1}} \leq A_{α_{2}}$ , т.е. мощность подмножества $A_{α_{1}}$ не больше мощности подмножества $A_{α_{2}}$ .

Теорема о декомпозиции. Всякое нечеткое множество $A$ , может быть представлено объединением всех своих $α$ -уровневых множеств:

$A = \underset{α \in [0; 1]}{\cup} \{α / x ∣ x \in A_{α}\}$ .

Пример: Нечеткое множество $A = 0,1 / x_{1} + 0 / x_{2} + 0,7 / x_{3} + 1 / x_{4}$ представимо в виде объединения всех своих $α$ -уровневых множеств $A_{0} = \{x_{1}; x_{2}; x_{3}; x_{4}\}$ , $A_{0,1} = \{x_{1}; x_{3}; x_{4}\}$ , $A_{0,7} = \{x_{3}; x_{4}\}$ , $A_{1} = \{x_{4}\}$ :

A = \{0 / x ∣ x \in A_{0}\} \cup \{0,1 / x ∣ x \in A_{0,1}\} \cup \{0,7 / x ∣ x \in A_{0,7}\} \cup \{1 / x ∣ x \in A_{1}\}

$A = (0 / x_{1} + 0 / x_{2} + 0 / x_{3} + 0 / x_{4}) \cup (0,1 / x_{1} + 0,1 / x_{3} + 0,1 / x_{4}) \cup (0,7 / x_{3} + 0,7 / x_{4}) \cup (1 / x_{4})$ .

$A = 0,1 / x_{1} + 0 / x_{2} + 0,7 / x_{3} + 1 / x_{4}$ .