3.4. Анализ динамики нечетких САУ

Анализ динамики гибридных и адаптивных нечетких САУ существенно осложняется тем, что алгоритмы управления, увязанные в интеллектуальных системах данного класса с процедурами нечеткой коррекции и, соответственно, нечеткой адаптации, имеют аналитическое описание, не позволяющее интерпретировать динамику систем алгебраическими, дифференциальными или интегральными уравнениями. Данная особенность существенно сужает круг возможных методов, которые могут применяться для исследования динамики гибридных и адаптивных нечетких САУ и, фактически оставляет исследователю только один из них: метод математического (аналитического или имитационного, в зависимости от сложности описания объекта управления) моделирования.

Относительно САУ с нечеткими контроллерами положение не столь безнадежно. В системах данного класса нечеткий контроллер является самостоятельным функционально законченным элементом, вырабатывающим на основе четких измеряемых входных сигналов, характеризующих состояние объекта, такой же четкий измеряемый выходной сигнал управления объектом. Поэтому помимо уже упомянутого подхода к исследованию динамики нечетких САУ при помощи моделирования возможно получение зависимости (характеристики) нечеткого контроллера, однозначно связывающей входные и выходные сигналы данного элемента САУ, и последующее использование этой характеристики при исследовании динамки САУ традиционными методами теории автоматического управления. Законченной методики анализа динамики САУ с нечеткими контроллерами методами классической теории управления в данный момент пока еще не существует. В каждом отдельном случае необходимо рассматривать конкретную нечеткую САУ и, в зависимости от реализации структуры нечеткого контроллера и сложности описания объекта управления, выбирать тот или иной метод исследования динамики системы.

Далее приведены примеры, наглядно демонстрирующие концепцию применения данного подхода к исследованию динамики САУ с нечеткими контроллерами, который заключается в получении описания зависимости вход-выход нечеткого контроллера, пригодного для последующего использования в рамках того или иного метода теории автоматического управления.

Пример. Рассмотрим САУ с нечетким контроллером, предназначенную для стабилизации температуры в камере газовой печи (рис.3.18(а)).

Рис.3.18(а). Функциональная схема нечеткой САУ температурой печи

Обобщенный объект управления включает газовую горелку, камеру печи и датчик температуры в камере печи. Сигнал t с датчика температуры поступает на сумматор, где сравнивается с сигналом $t_{зад}$ , задающим требуемую температуру в камере печи. Сигнал ошибки e поступает на вход нечеткого контроллера, который в соответствии с заложенным проектировщиком алгоритмом нечеткого вывода вырабатывает сигнал управления u , подаваемый на вход полупроводникового усилителя. Полупроводниковый усилитель при помощи напряжения $u_{дв}$ управляет двигателем постоянного тока, который в свою очередь через редуктор изменяет угол поворота λ клапана расхода топлива газовой горелки. Инерционностью полупроводникового усилителя и датчика температуры, которые на порядки меньше постоянных времени остальных элементов САУ, можно пренебречь. Двигатель постоянного тока с редуктором представляет последовательное соединение апериодического и интегрирующего звеньев, поскольку выходным сигналом двигателя является угол поворота клапана газовой горелки и электромагнитной постоянно времени двигателя можно пренебречь. Обобщенный объект управления описывается апериодическим звеном.

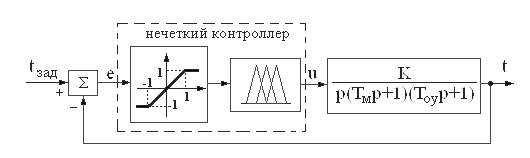
Рис.3.18(б). Структурная схема нечеткой САУ температурой печи

Структурная схема нечеткой САУ представлена на рис.3.18(б), где K – суммарный коэффициент усиления, являющийся произведением коэффициентов усиления полупроводникового усилителя, двигателя, редуктора и обобщенного объекта управления, $T_{м}$ – электромеханическая постоянная времени электродвигателя, $T_{оу}$ – постоянная времени обобщенного объекта управления.

Система нечеткого вывода fuzzy-регулятора построена следующим образом:

лингвистическая переменная «сигнал ошибки», соответствующая выходу сумматора , на входе нечеткого контроллера по модулю ограничивается нелинейным элементом с насыщением и задается термами NB-«отрицательная большая», NM-«отрицательная средняя», Z-«нулевая», PM-«положительная средняя», PB-«положительная большая»;
лингвистическая переменная «управление», соответствующая выходу нечеткого контроллера , задается термами NB-«отрицательная большая», NM-«отрицательная средняя», Z-«нулевая», PM-«положительная средняя», PB-«положительная большая»;
термы лингвистических переменных «сигнал ошибки» и «управление» задаются нечеткими множествами (рис.3.19(а,б));

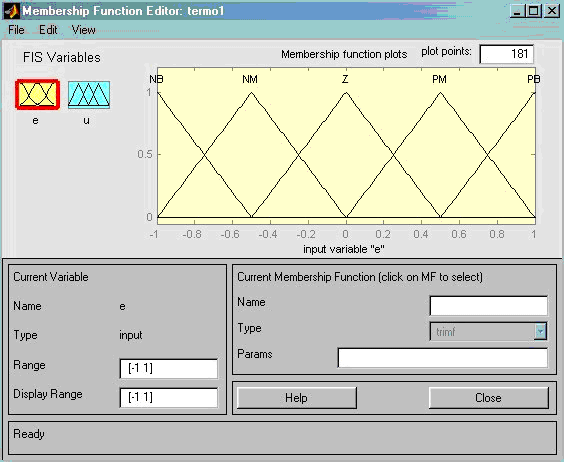
Рис.3.19(а). Функции принадлежностей лингвистических переменных, определяющих нечеткое представление входного и выходного сигналов нечеткого контроллера

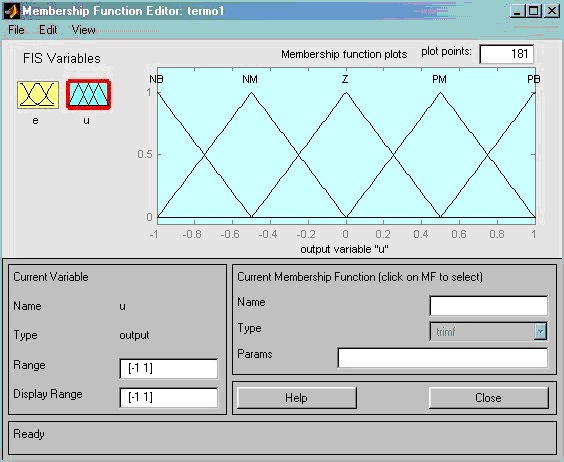
Рис.3.19(б). Функции принадлежностей лингвистических переменных, определяющих нечеткое представление входного и выходного сигналов нечеткого контроллера

эвристические правила, применяющиеся при регулировании температуры в камере печи посредством поворота вентиля газовой горелки задаются базой продукционных правил, на которой реализован алгоритм нечеткого вывода Мамдани (рис.3.20 (а, б)).

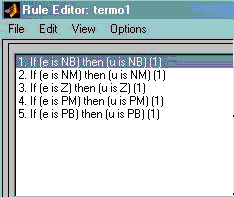
Рис.3.20(а). База продукционных правил нечеткого контроллера САУ температурой печи, реализующего алгоритм нечеткого вывода Мамдани

Рис.3.20(б). База продукционных правил нечеткого контроллера САУ температурой печи, реализующего алгоритм нечеткого вывода Мамдани

Очевидно, это видно даже исходя из визуального осмотра графика, что полученную путем моделирования статическую характеристику можно аппроксимировать тремя отрезками прямых с коэффициентами наклона $k_{1} = 1$ , $k_{2} = \frac{1}{3}$ и $k_{1} = 1,25$ соответственно (рис.3.21), т.е. дать ей следующее аналитическое описание:

u = \{\begin{matrix} e, при |e| ≤ 0,5; \\ \frac{1}{3} e+0,5, при 0,5 < e ≤ 0,8; \\ \frac{1}{3} e - 0,5, при -0,8 ≤ e < -0,5; \\ 1,25 e - 0,4, при 0,8 < e ≤ 1; \\ 1,25 e + 0,4, при -1 ≤ e < ≤ - 0,8; \\ 0,85, при e > 1; \\ - 0,85, при e < -1; \end{matrix}

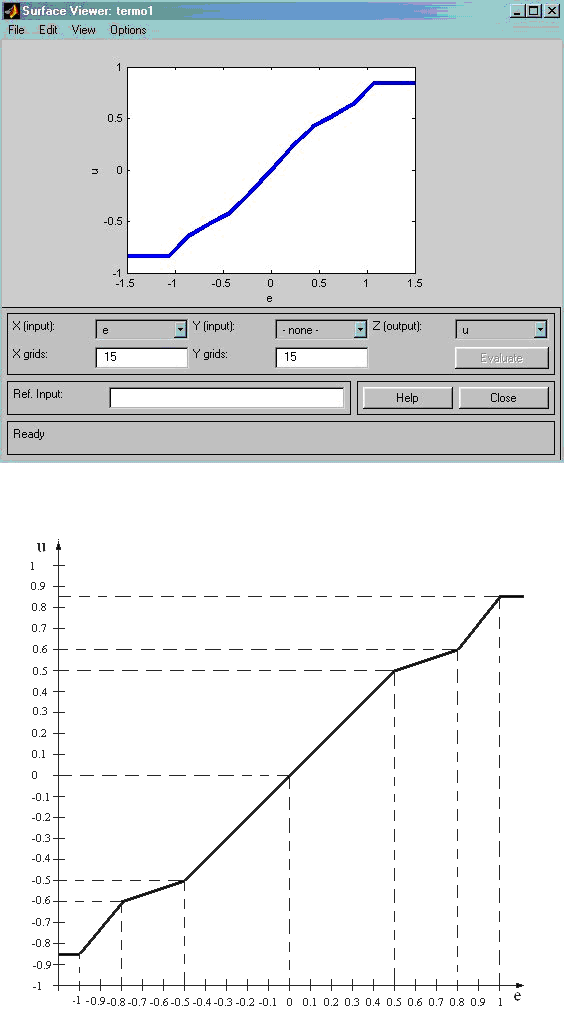
Рис.3.21. Статическая характеристика нечеткого контроллера САУ температурой печи и ее аппроксимация отрезками прямых

Такое представление нечеткого контроллера позволяет перейти от исходной нечеткой САУ (рис.3.18) к эквивалентной нелинейной САУ (рис.3.22), что делает возможным применение методов теории нелинейных систем для анализа динамики рассматриваемой системы автоматического управления [31].

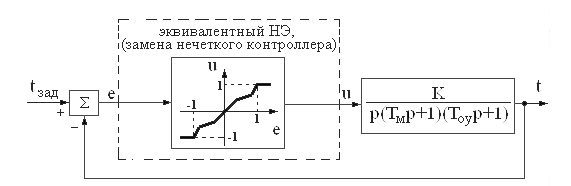
Рис.3.22. Эквивалентная нелинейная САУ

Проведем анализ устойчивости исходной САУ с нечетким контроллером методом Попова. Аппроксимированная статическая характеристика нечеткого контроллера (рис.3.21) не выходит за пределы сектора, ограниченного осью абсцисс и прямой $u = k_{1} e$ . Согласно критерию Попова, эквивалентная нелинейная система (рис.3.22) асимптотически устойчива, если через точку на комплексной плоскости $(-\frac{1}{k_{1}};0)$ можно провести прямую, такую, что преобразованная КЧХ линейной части системы $W_{д} (jω) = Re(W_{д} (jω) + wIm(W_{д} (jω))$ лежит справа от прямой. Зададимся следующими параметрами модели $T_{м} = 1 с$ , $T_{оу} = 40 с$ и построим для линейной части системы $W_{д} (s) = \frac{K}{s(T_{э}s+1)(T_{оу}s+1)}$ семейство преобразованных КЧХ $W^{*} (jω))$ (рис.3.23). Анализ годографов показывает, что через точку на комплексной плоскости $(-\frac{1}{k_{1}};0) |_{k_{1}=1} = (-1;0)$ можно провести прямую, проходящую слева от годографа преобразованной КЧХ, только если коэффициент усиления линейной части системы $K < 1$ . В противном случае эквивалентная нелинейная САУ не является асимптотически устойчивой и в ней наблюдаются автоколебания.

Рис.3.23. Семейство модифицированных КЧХ линейной части системы

Результаты моделирования работы исходной нечеткой САУ при различных коэффициентах усиления линейной части системы, представленные на рис.3.24, подтверждают данные, полученные методом Попова: точка $K = 1,03$ является критической точкой при переходе через которую колебания в нечеткой САУ становятся незатухающими. Ошибка $3 %$ в определении критического коэффициента усиления линейной части системы обусловлена погрешностями, возникающими при моделировании, а также при замене экспериментально полученной статической характеристики ее кусочно-линейной аппроксимацией (3.1).

При моделировании работы исходной нечеткой САУ с параметрами модели $K = 2$ , $T_{м} = 1 с$ , $T_{оу} = 40 с$ обобщенного объекта управления в установившемся режиме наблюдаются автоколебания с амплитудой $a = 2^{o} C$ и частотой $ω= = 0,157 c^{-1}$ (рис.3.24). Можно вычислить аналитически параметры автоколебаний, наблюдаемых в исходной нечеткой САУ, применив для исследования эквивалентной нелинейной САУ метод гармонической линеаризации.

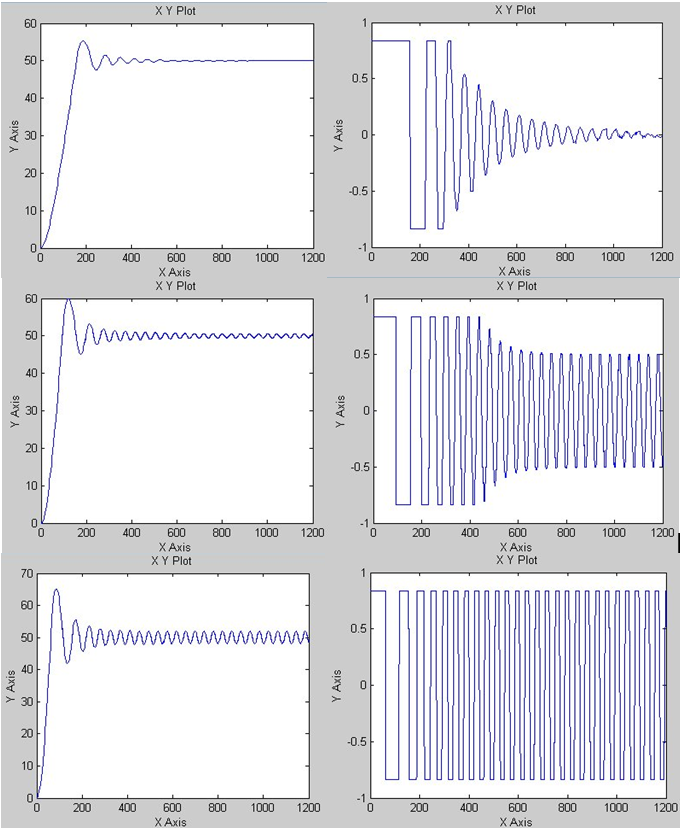
Рис.3.24. Переходный процесс в исходной нечеткой САУ температурой печи при пуске объекта управления и выводе его на установившийся режим $t_{зад} = 100^{o}C$ ; слева – температура t ; справа – управление u ; абсцисса – время переходного процесса; вверху – переходные процессы при K=5 ; в центре – при K=1 ; внизу – при K=2 ;

Комплексный коэффициент усиления эквивалентного нелинейного элемента может быть выведен аналитически, с использованием полученной в результате моделирования и аппроксимированной кусочно-линейными функциями статической характеристики эквивалентного нелинейного элемента (рис.3.21). Ввиду громоздкости опущены промежуточные вычисления процесса вывода коэффициентов гармонической линеаризации $q(a,ω)$ , $q^{'} (a,ω)$ эквивалентного нелинейного элемента (3.1), определяющих передаточную функцию $W_{н} (a,ω) = q(a,ω) +{jq}^{'}(a,ω)$ . Читатель может повторить процесс вывода коэффициентов гармонической линеаризации самостоятельно. Если не выводить формулы коэффициентов гармонической линеаризации в общем виде, а пользоваться конкретными численными значениями и исходить из того, что синусоидальный сигнал с амплитудой a>1 перекрывает все особенности статической характеристики эквивалентного нелинейного элемента, то в результате расчетов должны получиться значения коэффициентов $q(a,ω) = 0,262 +\frac{0,5}{a}, q^{'} (a,ω) =0$ . Второй коэффициент гармонической линеаризации тождественно равен нулю, поскольку эквивалентный нелинейный элемент имеет однозначную статическую характеристику. Воспользовавшись методом Гольдфарба, можно найти амплитуду и частоту гармонических колебаний, устанавливающихся в системе. Уравнение Гольдфарба $W_{н} (a,ω) = \frac{-0,5}{W_{л}(a,ω)}$ , где $W_{н} (a,ω) = W_{н} (a) = 0,265 +\frac{0,5}{a}, W_{л} (s) = \frac{K}{jω(T_{э}jω+1)(T_{оу}jω+1)}$ . Приравняв действительные и мнимые части правой и левой части уравнения Гольдфарба, находим $ω= = 0,158 c^{-1}$ , $a = {2,025}^{o} C$ , что вполне согласуется с данными, полученными ранее в результате моделирования работы САУ с нечетким контроллером.

Рассмотрим, теперь случай, когда в нечеткой САУ используется нечеткий контроллер с несколькими входами.

Пример. Рассмотрим САУ с двухвходовым нечетким контроллером, предназначенную для стабилизации температуры в камере газовой печи (рис.3.25), которая отличается от системы, разобранной в предыдущем примере, конфигурацией нечеткого контроллера. Сигналы ошибки e и производной сигнала ошибки e поступают на вход нечеткого контроллера, который в соответствии с заложенным проектировщиком алгоритмом нечеткого вывода вырабатывает сигнал управления u . Следует ожидать, что реализация нечеткого управления, при котором управляющее воздействие выбирается исходя из величины не только самой ошибки e , но и ее производной e , позволит обеспечить более высокое качество регулирования и избежать в системе автоколебаний, возникающих в предыдущем случае.

Рис.3.25. Функциональная схема нечеткой САУ температурой печи

Система нечеткого вывода fuzzy-регулятора:

лингвистическая переменная «сигнал ошибки», соответствующая выходу сумматора , на входе нечеткого контроллера по модулю ограничивается нелинейным элементом с насыщением и задается термами NB-«отрицательная большая», NM-«отрицательная средняя», NS-«отрицательная малая», Z-«нулевая», PS-«положительная малая», PM-«положительная средняя», PB-«положительная большая»;
лингвистическая переменная «производная сигнала ошибки», соответствующая выходу блока дифференцирования , на входе нечеткого контроллера по модулю ограничивается нелинейным элементом с насыщением и задается термами NB-«отрицательная большая», NM-«отрицательная средняя», NS-«отрицательная малая», Z-«нулевая», PS-«положительная малая», PM-«положительная средняя», PB-«положительная большая»;
лингвистическая переменная «управление», соответствующая выходу нечеткого контроллера , задается термами NB-«отрицательная большая», NM-«отрицательная средняя», NS-«отрицательная малая», Z-«нулевая», PS-«положительная малая», PM-«положительная средняя», PB-«положительная большая»;
термы лингвистических переменных «сигнал ошибки», «производная сигнала ошибки», «управление» и эвристические правила задаются следующим образом (рис.3.26(а,б))

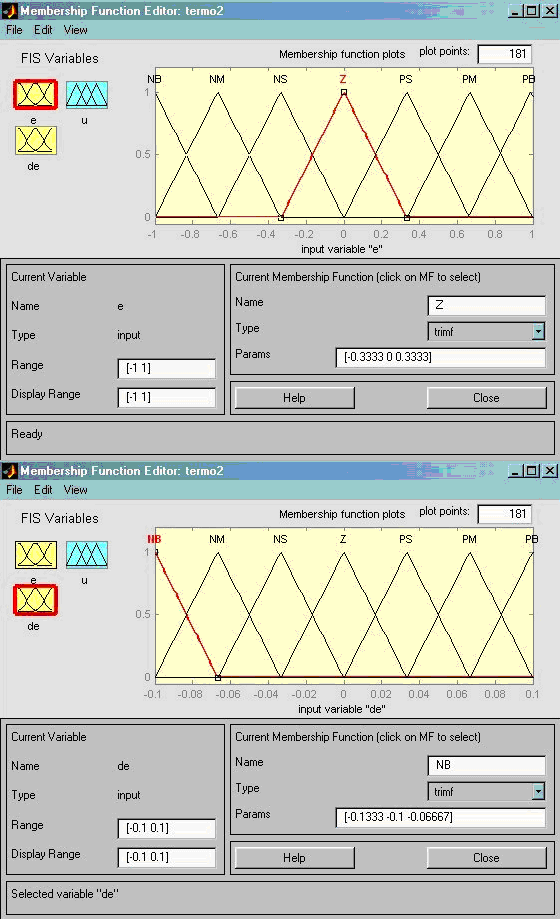
Рис.3.26(а). Функции принадлежностей лингвистических переменных и база продукционных правил нечеткого контроллера САУ температурой печи, реализующего алгоритм нечеткого вывода Мамдани

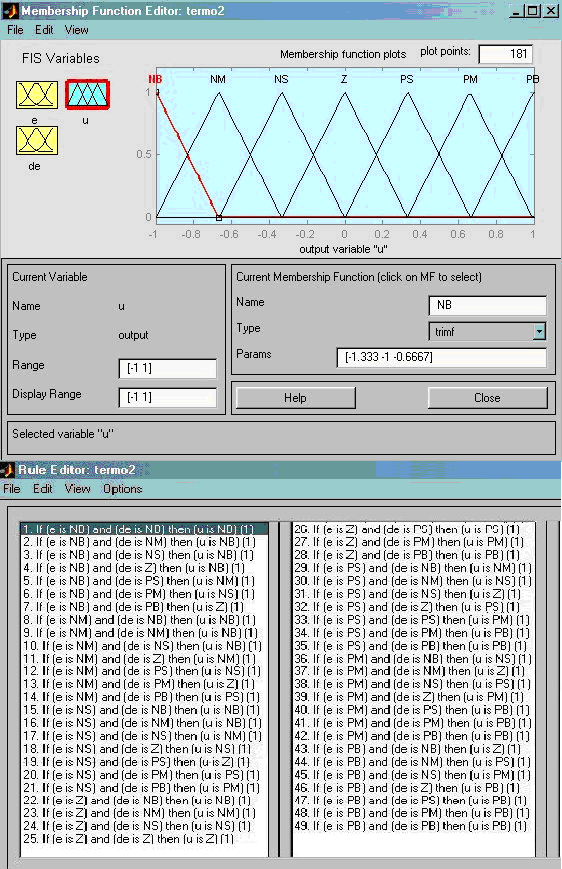
Рис.3.26(б). Функции принадлежностей лингвистических переменных и база продукционных правил нечеткого контроллера САУ температурой печи, реализующего алгоритм нечеткого вывода Мамдани

При моделировании работы исходной нечеткой САУ с параметрами модели $K = 2$ , $T_{м} = 1 c$ , $T_{оу} = 40 c$ обобщенного объекта управления в установившемся режиме автоколебания отсутствуют (рис.3.27), т.е. увеличение количества входов нечеткого контроллера и расширение базы продукционных правил привело к повышению качества управления (увеличению быстродействия и устойчивости системы ). Анализ графика управления, который на протяжении переходного процесса демонстрирует высокую скорость переключения управления между двумя значениями с частотой практически совпадающей с шагом моделирования системы, переключения позволяет сделать предположение, что рассматриваемая САУ с нечетким контроллером система работает в режиме, качественно напоминающем скользящий режим функционирования нелинейных систем.

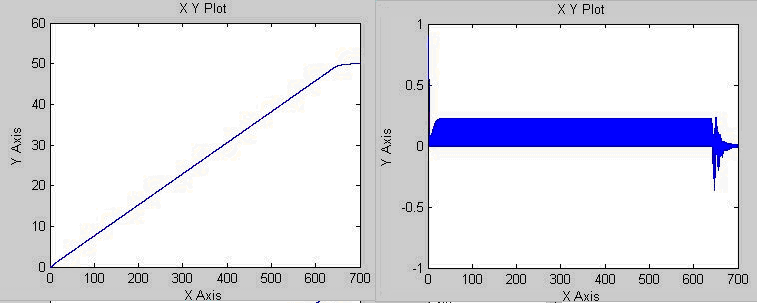
Рис.3.27. Переходный процесс в исходной нечеткой САУ температурой печи при пуске объекта управления и выводе его на установившийся режим $t_{зад} = 100^{o} C$ ; слева – температура t ; справа – управление u ; абсцисса – время переходного процесса

Поскольку нечеткий контроллер имеет два входа, один из которых зависит от другого, и один выход, то, формально включив блок дифференцирования в структуру нечеткого контроллера, его можно рассматривать как эквивалентный нелинейный элемент с одним входом и одним выходом (рис.3.28).

Следует обратить внимание на то, что если входные сигналы нечеткого контроллера независимы друг от друга, то приведенный выше способ эквивалентной замены неприменим, т.е. невозможно перейти от исходного нечеткого контроллера к эквивалентному нелинейному элементу с одним входом и одним выходом.

Рис.3.28. Структурная схема нечеткой САУ температурой печи

Поскольку эквивалентный нелинейный элемент в данном случае обладает свойствами как статической, так и динамической нелинейности, то эквивалентная нелинейная САУ будет выглядеть следующим образом (рис.3.29)

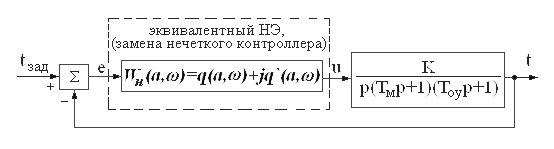
Рис.3.29. Эквивалентная нелинейная САУ

Коэффициенты гармонической линеаризации $q(a,ω)$ , $q^{'} (a,ω)$ можно получить в численном виде посредством моделирования работы нечеткого контроллера (считая, что блок дифференцирования входит в его состав), подавая на его вход синусоидальные сигналы $e = asin(ωt)$ различной амплитуды и частоты, выделяя затем на выходе нечеткого контроллера первую гармонику и сравнивая ее амплитуду и фазу с амплитудой входной синусоиды. Таким образом можно получить $q(a,ω)$ , $q^{'} (a,ω)$ заданные таблично, далее решить уравнение Гольдфарба графоаналитическим методом и, таким образом, найти амплитуду и частоту гармонических колебаний, устанавливающихся в системе. Либо можно получить приблизительное аналитическое представление $q(a,ω)$ , $q^{'} (a,ω)$ аппроксимировав по точкам численное представление $q(a,ω)$ , $q^{'} (a,ω)$ и далее решить уравнение Гольдфарба аналитически.

Таким образом, опираясь на рассмотренные примеры, можно дать следующие общие рекомендации по исследованию динамики САУ с нечеткими контроллерами:

если нечеткий контроллер имеет один вход и один выход, то его можно рассматривать как эквивалентный нелинейный безынерционный элемент (статическую нелинейность), что дает возможность получить его статическую характеристику, коэффициенты гармонической линеаризации и использовать их для дальнейшего исследования динамики системы известными методами теории управления;
если нечеткий контроллер имеет несколько зависимых входов, например двухвходовый нечеткий контроллер с входными сигналами отклонения и скорости изменения отклонения , и один выход, то его можно рассматривать как эквивалентный нелинейный элемент, обладающий свойствами как статической, так и динамической нелинейности, что дает возможность при помощи моделирования получить в численном виде коэффициенты гармонической линеаризации эквивалентного нелинейного элемента и использовать их для дальнейшего исследования динамики системы известными методами теории управления;
если нечеткий контроллер имеет несколько независимых входов и выходов, то описание его динамики указанными выше способами становится невозможным, поскольку нельзя заменить исходный нечеткий контроллер эквивалентным нелинейным элементом, т.е. упомянутые методики неприменимы для многомерных нелинейных систем.

Следует отметить тот факт, что исследование динамики САУ с нечетким контроллером исключительно аналитически, без использования моделирования невозможно, даже в случае, если нечеткий контроллер можно заменить эквивалентным нелинейным элементом. Это обусловлено тем, что при замене нечеткого контроллера эквивалентным нелинейным элементом характеристики эквивалентного нелинейного элемента (статическую характеристику или эквивалентный коэффициент усиления) можно получить только путем моделирования работы нечеткого контроллера и никак иначе.